
Excelling in high-level math evaluations requires more than memorizing formulas; it demands critical thinking, practical application, and a strategic approach to problem-solving. These tests are designed to assess not just knowledge but also adaptability and accuracy under pressure.
Understanding the types of problems presented and developing a systematic method for tackling them can significantly enhance your performance. Recognizing patterns, avoiding common errors, and efficiently managing your time are essential components of success.
This article offers a comprehensive approach to mastering advanced topics, enhancing your preparation strategies, and boosting your confidence. With careful planning and targeted practice, you can navigate complex questions and achieve your academic goals.
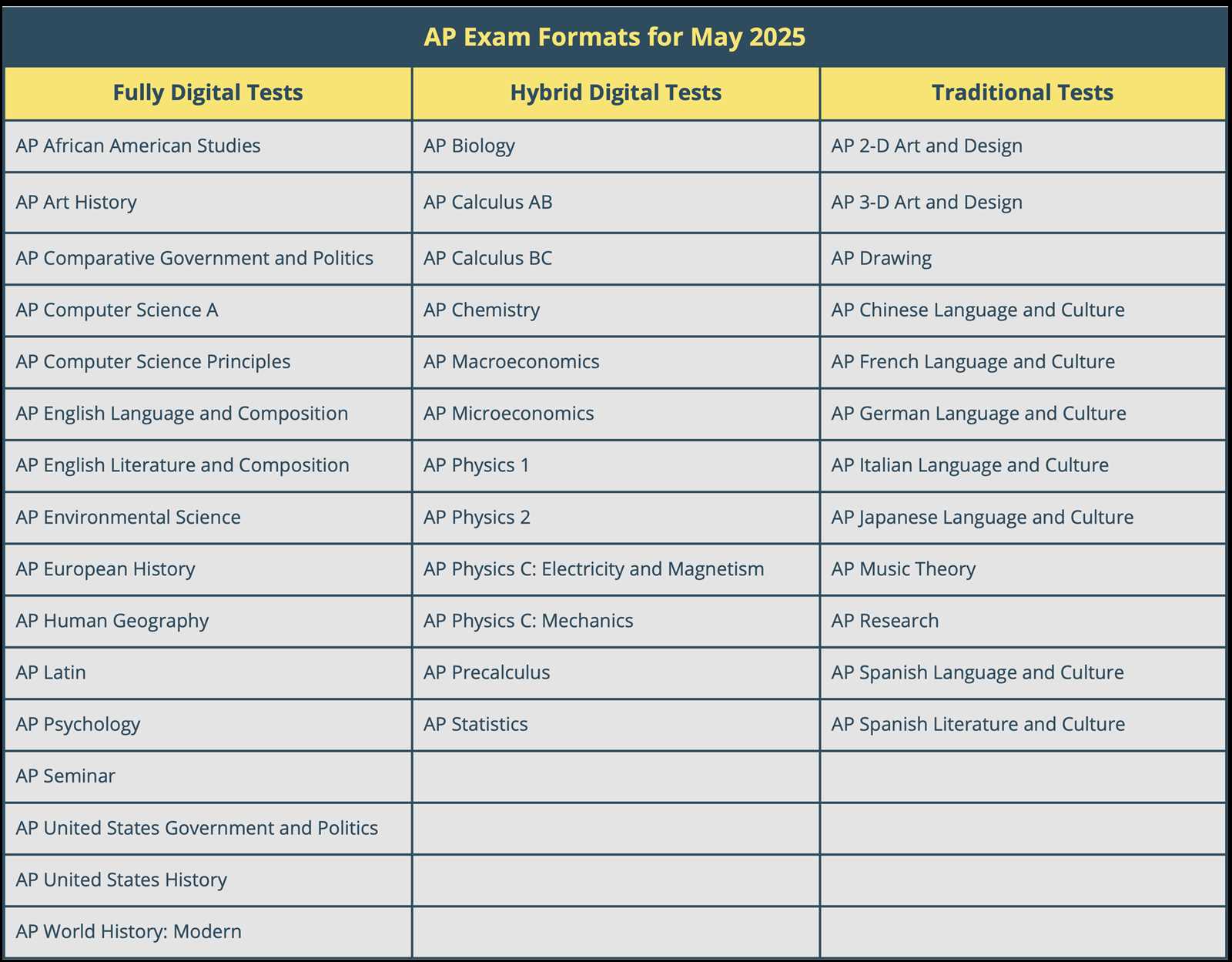
2025 AP Calculus BC Exam Overview
The AP exam for advanced mathematics tests students’ abilities to apply complex concepts in various problem-solving scenarios. It assesses both theoretical understanding and practical application, requiring a deep grasp of a wide range of topics from limits and derivatives to integrals and series.
This assessment is structured to include both problem-solving and analytical reasoning tasks. It challenges students to think critically and work efficiently, testing their ability to navigate questions that require both speed and accuracy.
Preparation for such an exam involves not only reviewing key topics but also honing the skills necessary to tackle difficult questions under time constraints. A well-rounded study approach, focusing on both conceptual mastery and practical problem-solving, is essential for achieving success.
What to Expect in Multiple Choice

The assessment will feature a range of questions designed to evaluate your understanding of advanced mathematical concepts. Expect problems that require both analytical skills and the ability to apply formulas in various contexts. The questions will test not just memorization but also your capacity to solve complex problems quickly and accurately.
Questions will vary in difficulty, with some requiring deep knowledge of specific topics and others testing your ability to apply concepts in unfamiliar scenarios. You’ll need to demonstrate proficiency in working with functions, derivatives, integrals, and series, among other advanced mathematical areas.
Each problem is designed to assess your problem-solving approach, so focus on identifying the most efficient methods for tackling different types of questions. The format encourages quick thinking and the ability to recognize patterns, making time management a crucial factor in your success.
Key Concepts for Success in Calculus
Mastering the essential principles of advanced mathematics is crucial for performing well in any high-level exam. A strong foundation in core topics such as limits, rates of change, and accumulation is necessary for success. Understanding how to approach problems methodically and applying the right techniques to different scenarios can significantly improve your problem-solving efficiency.
In particular, a deep comprehension of functions and their properties, as well as the ability to manipulate derivatives and integrals, forms the backbone of the subject. Familiarity with series and sequences, and knowing when to use various tests for convergence, are also fundamental to tackling complex questions.
Additionally, the ability to interpret graphical representations and connect them to algebraic concepts is essential. A thorough understanding of these principles will not only enhance your exam performance but also equip you to handle the most challenging problems with confidence.
Time Management Tips for the Exam
Effective time management is essential for excelling in high-pressure testing environments. With limited time available for each section, it’s crucial to allocate your efforts strategically. Being able to prioritize tasks, avoid getting stuck on difficult problems, and ensure you have time to review your answers can make a significant difference in your performance.
Prioritize Easy Questions First
Start by answering the questions you find easiest. This will help build momentum and boost your confidence early on. By handling simpler problems first, you free up more time later for more complex tasks. It also allows you to quickly accumulate points before tackling harder sections.
Monitor Your Time Per Section
Each section of the test comes with its own set of challenges. Make sure to keep track of time as you move through the exam. Set a personal time limit for each set of problems and stick to it. If you find yourself spending too much time on a single question, move on and come back to it later if needed. This will ensure you cover all areas and reduce the risk of running out of time.
Analyzing Calculus Graphs Quickly
When facing problems that involve graphical representations, the ability to interpret and analyze them swiftly is key to answering questions efficiently. Graphs are a valuable tool in understanding mathematical concepts, and being able to extract important information quickly will save you time during the exam. Knowing how to identify key features, such as critical points, inflection points, and asymptotes, can provide insight into the behavior of a function.
Key Features to Identify
- Critical Points: These are points where the derivative is zero or undefined, often indicating local maxima, minima, or saddle points.
- Intervals of Increase/Decrease: Identifying where the graph rises or falls helps in understanding the behavior of the function.
- Inflection Points: Points where the graph changes concavity, which may indicate changes in the rate of growth or decay.
- Asymptotes: Vertical or horizontal asymptotes indicate the behavior of the function as it approaches infinity or a specific value.
Efficient Graph Analysis Strategies

- Start by identifying the endpoints of the graph and the overall behavior at infinity.
- Look for any visible symmetry, which can help you predict the function’s properties without needing to perform extensive calculations.
- Focus on key points like intercepts, peaks, and troughs that provide insight into the function’s general shape and behavior.
Common Mistakes in Multiple Choice
When taking exams that involve problem-solving with set options, it’s easy to fall into certain traps that can lead to incorrect selections. Many students make errors not due to a lack of understanding, but because of small mistakes or misinterpretations of the question. Recognizing and avoiding these common pitfalls can significantly improve your overall performance.
- Rushing Through Questions: One of the most frequent errors is rushing to choose an answer without carefully reading the problem or all the options. This can lead to misinterpretations or skipping over important details.
- Overlooking Units: Failing to account for units of measurement or misinterpreting them can cause you to select the wrong response. Always double-check the units when solving problems.
- Skipping Key Steps: In an effort to save time, students often skip important intermediate steps. This can lead to mistakes, especially when the problem requires several calculations or logical steps to reach the solution.
- Second-Guessing: Another common mistake is second-guessing yourself after already selecting an answer. Overthinking can lead to changing the correct choice to an incorrect one, especially if you don’t have a clear reason for altering your answer.
- Misreading Graphs or Diagrams: Graphs and visual aids often contain crucial information. Misinterpreting these visuals can lead to errors, particularly when questions ask about trends or specific features like intercepts or slopes.
Strategies for Solving Derivative Questions

When tackling problems that involve derivatives, a clear and systematic approach is essential to solving them correctly and efficiently. Understanding the underlying principles and applying the right techniques can help you navigate through even the most challenging questions. By breaking down the problem and using key strategies, you can reduce mistakes and save time during the exam.
Understand the Problem and Identify the Function
Before diving into calculations, carefully read the question to identify what is being asked. Often, derivative problems will involve functions that require you to find the rate of change at specific points or over intervals. Recognizing whether you need to apply the product, quotient, or chain rule is crucial to solving the problem correctly.
Apply the Correct Differentiation Rule

Once you’ve identified the type of function, choose the appropriate rule for differentiation. For example, if you’re dealing with a product of functions, the product rule should be used. If the function involves a composite function, the chain rule will be necessary. Practice using these rules fluently to quickly identify the most effective approach.
Integrals and Antiderivatives Explained
Understanding the connection between integrals and antiderivatives is fundamental to solving problems in advanced mathematics. Both concepts involve reversing the process of differentiation, but they apply in different contexts and use distinct methods. Grasping their relationship will not only help in solving specific problems but also deepen your overall understanding of how functions behave.
An antiderivative of a function is essentially the inverse operation of differentiation. Given a function, the antiderivative is another function whose derivative equals the original function. In contrast, an integral represents the accumulation of a quantity over an interval, which can be seen as the area under a curve. While both processes involve finding a function from its rate of change, the integral focuses on total accumulation, and the antiderivative focuses on reversing the differentiation process.
In practice, solving these problems involves recognizing when to apply each technique. Antiderivatives often come into play when you’re asked to find a general or particular solution to a differential equation. Integrals, on the other hand, are used when you need to calculate the area under a curve or determine the total accumulated quantity across a specific interval.
Approaching Series and Sequences Efficiently
When faced with problems involving sequences and series, it’s essential to approach them strategically in order to identify patterns and apply the appropriate methods. Both sequences and series play a central role in mathematical analysis, often requiring careful attention to detail and a solid understanding of convergence and summation techniques. Recognizing key properties and applying the right formulas will make these problems easier to tackle efficiently.
To solve problems related to series and sequences, it is important to identify whether the given sequence is arithmetic, geometric, or involves more complex behavior. For example, arithmetic sequences have a constant difference between terms, while geometric sequences involve a constant ratio. Recognizing these patterns early can guide you toward the correct approach, whether you need to find the nth term or sum the series.
| Sequence Type | Formula | Key Property |
|---|---|---|
| Arithmetic | a_n = a_1 + (n-1) * d | Constant difference between terms |
| Geometric | a_n = a_1 * r^(n-1) | Constant ratio between terms |
| Harmonic | a_n = 1/n | Terms decrease in reciprocal fashion |
For series, when the terms of the sequence are summed, the task becomes identifying whether the series converges or diverges. For convergent series, understanding the tests for convergence such as the ratio test, root test, or integral test is key. These tests help determine whether the sum approaches a finite value or continues to grow indefinitely.
Understanding Limits and Continuity Problems

When dealing with problems involving behavior at specific points or over intervals, understanding limits and continuity is crucial. These concepts are foundational in determining how functions behave as they approach certain values, whether those values are finite or infinite. Grasping the key ideas behind limits and continuity will enable you to solve a wide range of problems, especially those that deal with function behavior near discontinuities or asymptotes.
Limits: How Functions Approach Values
Limits describe the behavior of a function as it approaches a certain point from either direction. They allow us to understand what happens to a function as the input values get closer to a particular value, even if the function doesn’t explicitly reach that value. This is particularly important when dealing with discontinuities or undefined points in the function. Analyzing limits involves checking both one-sided limits (approaching from the left or right) and overall behavior at a given point.
Continuity: Smoothness of a Function
A function is continuous at a point if its graph has no breaks, jumps, or holes at that point. To be continuous, a function must satisfy three key conditions: the function must be defined at that point, the limit must exist, and the limit must equal the function’s value at that point. Understanding continuity helps identify where a function may exhibit sudden changes in value or undefined behavior.
Using the Calculator During the Exam
When taking an exam that permits the use of a calculator, it’s essential to know when and how to leverage this tool effectively. The calculator can significantly speed up certain calculations, but its proper usage requires understanding which tasks it can assist with and where it may not be as helpful. Using it efficiently can save time, reduce errors, and improve overall performance during the test.
When to Use the Calculator
Here are some situations where the calculator can be particularly useful:
- Performing complex arithmetic or large calculations that would be time-consuming by hand.
- Evaluating definite integrals or sums that require precise numerical results.
- Checking the solutions to differential equations or solving systems of equations.
- Graphing functions to visually inspect trends, intersections, or limits.
Limitations of the Calculator
While the calculator can aid in numerous calculations, there are certain limitations to its use during the exam:
- It cannot replace the understanding of fundamental concepts or the ability to solve problems without technological assistance.
- Relying too heavily on the calculator may lead to overlooking simple steps or misinterpreting the problem.
- Some problems may require an analytical approach that doesn’t involve a calculator, such as proving theorems or applying specific mathematical rules.
Mastering Fundamental Theorems of Calculus
The fundamental theorems of analysis form the backbone of many problems in higher mathematics. They establish the connection between derivatives and integrals, allowing you to switch between finding rates of change and calculating total accumulated quantities. Mastery of these theorems is critical, as they not only simplify complex problems but also provide a deeper understanding of mathematical relationships.
The First Fundamental Theorem
The first theorem connects the process of differentiation with that of integration. It states that if a function is continuous over a closed interval, then its definite integral can be calculated using any antiderivative of the function. In other words, it tells us how to compute the area under a curve by evaluating the difference between the values of an antiderivative at the endpoints of the interval.
The Second Fundamental Theorem
The second theorem focuses on the reverse process: it provides a way to differentiate an integral with respect to its upper limit. This theorem is important because it allows you to compute the derivative of a function defined by an integral, which has numerous applications in real-world problems involving rates of change and accumulation. Understanding this theorem is crucial for simplifying and solving differential equations and other advanced problems.
How to Verify Your Answer Choices
Verifying your selected answers is an essential part of any exam preparation and test-taking strategy. The process ensures that the choices you’ve made are accurate and consistent with the problem requirements. Verification involves reviewing your calculations, confirming the logic behind your steps, and ensuring no mistakes or misinterpretations were made during problem-solving.
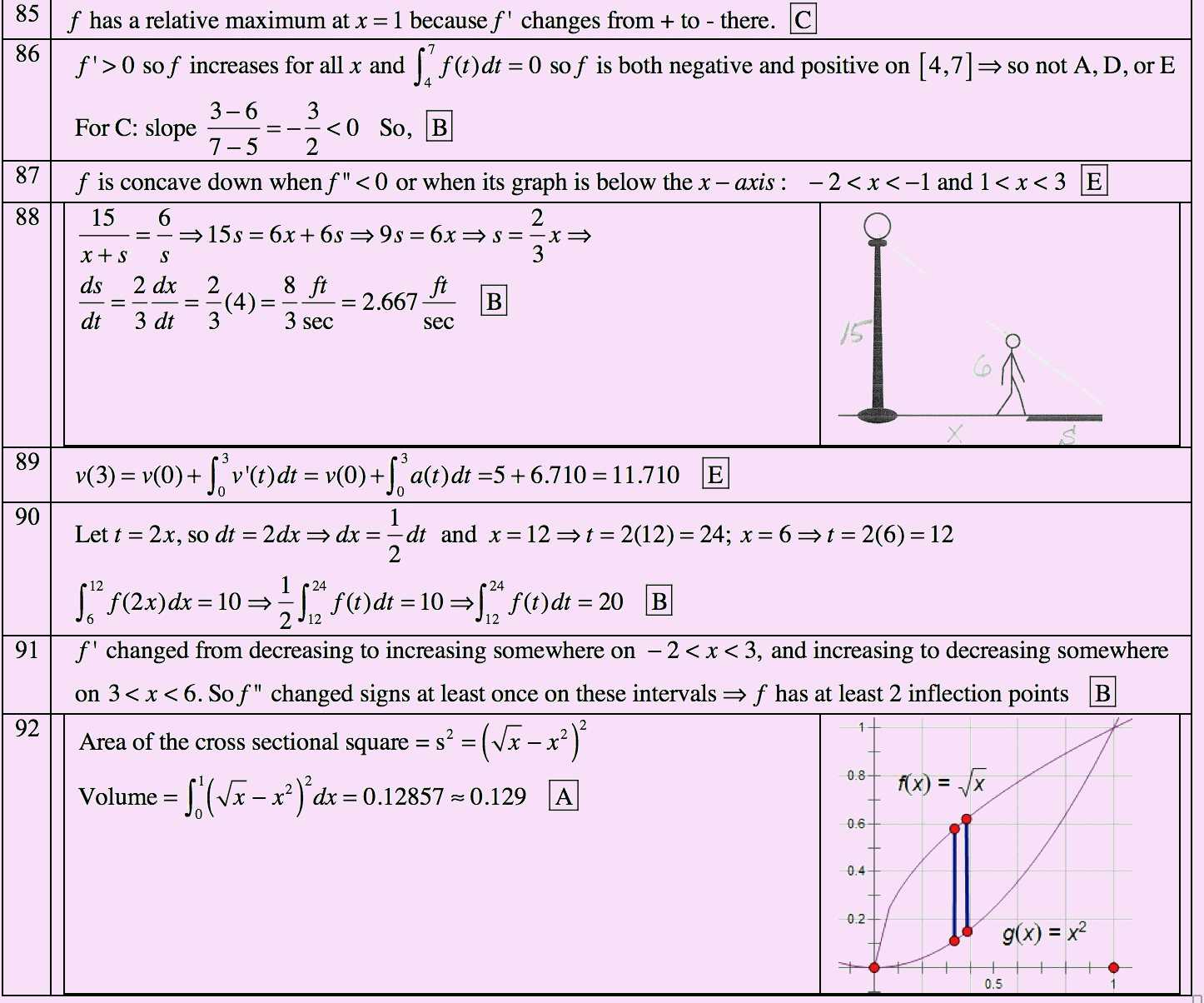
Steps for Effective Answer Verification
Follow these steps to double-check your selected options:
- Review the problem statement carefully to ensure you fully understand what is being asked.
- Revisit key formulas and concepts relevant to the question to ensure you’re applying the correct methods.
- Perform a quick mental check or estimation to see if your answer is reasonable in the context of the question.
- For calculation-based problems, rework the problem step-by-step to catch any arithmetic errors.
- If possible, plug your solution back into the original equation or context to verify that it satisfies all conditions.
Common Verification Pitfalls to Avoid
While verifying your answers, be mindful of these common mistakes:
- Rushing through the verification process, leading to oversight of small errors.
- Overlooking units or dimensions that may be crucial to the correctness of the solution.
- Misinterpreting the question and verifying answers based on incorrect assumptions.
- Neglecting to check for consistency between different parts of the problem (e.g., checking for overall logical consistency).
Preparing with Practice Problems and Solutions
One of the most effective ways to prepare for any exam is to engage with practice problems and work through detailed solutions. This method not only familiarizes you with the types of questions that may appear but also helps solidify your understanding of key concepts. Solving problems allows you to identify areas where you need further study while reinforcing the skills you have mastered.
Benefits of Practice Problems
Engaging with practice questions can provide several advantages:
- Strengthens problem-solving abilities by applying theory to actual problems.
- Increases familiarity with the format and structure of questions.
- Highlights weaknesses and areas that need further attention.
- Improves time management by practicing under timed conditions.
- Builds confidence as you review your solutions and identify patterns in problem types.
How to Use Solutions Effectively

While working through practice problems, it’s crucial to understand the solution process thoroughly:
- After attempting a problem, compare your solution to the provided one to identify mistakes and improve your methods.
- Pay attention to the step-by-step reasoning used in solutions, as this can reveal shortcuts or strategies you might have missed.
- Don’t just memorize the solutions; strive to understand the underlying principles that lead to those solutions.
- Use solutions as a learning tool to reinforce your approach and deepen your understanding of the material.
Essential Formulas for the AP Exam
Mastering key mathematical formulas is essential for success in any advanced mathematics exam. These formulas not only help streamline the problem-solving process but also provide the foundation for tackling complex questions. Having a strong grasp of the most commonly tested equations and concepts ensures that you can apply them quickly and effectively during the exam.
Critical Formulas to Remember
Here are some of the fundamental formulas and relationships you should be comfortable with for the exam:
| Formula | Description |
|---|---|
| Power Rule | Used to differentiate functions of the form f(x) = x^n. The derivative is f'(x) = n * x^(n-1). |
| Product Rule | For two functions f(x) and g(x), the derivative is f'(x) = f'(x) * g(x) + f(x) * g'(x). |
| Quotient Rule | For a quotient f(x) = g(x) / h(x), the derivative is f'(x) = (g'(x) * h(x) – g(x) * h'(x)) / (h(x))^2. |
| Chain Rule | Used for differentiating composite functions. If y = f(g(x))), then dy/dx = f'(g(x)) * g'(x). |
Integrals and Fundamental Theorem
Understanding integration and its connection to differentiation is crucial. The fundamental theorem of calculus states that if a function f is continuous on the interval [a, b], then:
- ∫(a to b) f(x) dx = F(b) – F(a), where F is the antiderivative of f.
- For solving definite integrals, make sure to correctly evaluate the limits.
Improving Problem-Solving Speed
One of the key factors to succeed in any timed examination is the ability to solve problems efficiently. The faster and more accurately you can navigate through questions, the better your chances of achieving a high score. By developing effective strategies, practicing consistently, and mastering key concepts, you can improve your speed without sacrificing accuracy.
Effective Strategies for Speed
Here are some practical tips to enhance your problem-solving efficiency:
- Familiarize Yourself with Common Patterns: Recognize frequently occurring problem types and develop a routine for tackling them.
- Work Backwards: For certain problems, especially those involving complex functions or equations, working backwards can be a time-saver.
- Prioritize Simpler Questions: Begin with questions you find easiest to boost confidence and avoid wasting time on difficult ones early in the exam.
- Skip and Return: If a question is taking too long, move on and return to it later when you have more time to analyze it properly.
Boosting Your Speed with Practice
Practicing under timed conditions is essential for improving your speed. Here are some ways to optimize your practice sessions:
- Timed Mock Exams: Simulate exam conditions by completing full-length practice tests within the allotted time frame.
- Focus on Problem Types: Concentrate on areas where you need improvement and work through problems of the same type until you can solve them faster.
- Track Your Progress: Keep a record of your performance and time spent on each problem, then analyze areas for improvement.
Dealing with Word Problems in Calculus
Word problems can be one of the most challenging aspects of an exam. They often require translating real-world scenarios into mathematical models, a skill that can take time to develop. The key to mastering these problems is to break them down systematically and identify the essential variables and relationships. By practicing these techniques, you can increase both your confidence and efficiency in solving these types of questions.
Understanding the Problem
The first step in tackling a word problem is understanding what is being asked. Carefully read the problem and identify the given information, what is unknown, and what needs to be solved. Often, word problems will describe a situation involving rates of change, areas, volumes, or other concepts, so recognizing the core idea is essential.
- Identify Known and Unknown Quantities: Look for key phrases that indicate the given values and those that need to be determined.
- Translate Words into Symbols: Convert the real-world situation into mathematical equations or functions.
- Understand the Context: Consider the scenario to ensure you are interpreting it correctly before proceeding.
Strategies for Solving Word Problems
Once you have a clear understanding of the problem, you can apply a methodical approach to solve it. Here are some strategies to help you solve word problems more effectively:
- Draw a Diagram: If applicable, draw a visual representation of the problem. Diagrams help clarify relationships between variables and simplify complex scenarios.
- Set Up Equations: Use the information provided in the problem to set up relevant equations or functions. These may involve derivatives, integrals, or algebraic expressions.
- Solve Step-by-Step: Take your time to solve the problem in logical steps, checking your work as you go.
- Check for Units: Ensure that the units make sense throughout the problem. Incorrect units can lead to errors in the final answer.
Final Exam Day Preparation Tips

The day of the exam can be stressful, but with the right preparation, you can feel confident and ready to perform at your best. Effective planning before the exam day is crucial for a smooth experience. This section offers valuable tips to help you manage your time, reduce stress, and approach the test with a clear mind.
Get Adequate Rest and Nutrition
One of the most important factors in exam performance is your physical and mental state. Getting a good night’s sleep and ensuring proper nutrition can significantly impact your ability to focus and think clearly during the test.
- Rest Well: Aim for 7-8 hours of sleep the night before the exam to ensure you’re alert and mentally sharp.
- Eat a Balanced Meal: Eat a healthy breakfast with proteins, whole grains, and fruits to fuel your brain for the exam.
- Avoid Caffeine Overload: While some caffeine is okay, too much can lead to jitters and an energy crash during the exam.
Organize Your Materials the Night Before
Preparing everything the night before will help you avoid any last-minute confusion or stress on exam day. Make sure all necessary materials are ready to go.
- Gather Necessary Items: Double-check that you have everything you need, such as pens, pencils, an eraser, a calculator, and your ID.
- Prepare Your Exam Kit: Pack your bag with any additional items you might need, like a water bottle, snacks, or a jacket.
- Review the Exam Details: Confirm the location, time, and format of the test to avoid any surprises.
Manage Time Effectively During the Exam
Proper time management can make a significant difference in your performance. Practicing time allocation during your review sessions can prepare you for the exam format.
| Task | Time Allocation |
|---|---|
| Quick Overview of the Exam | 5-10 minutes |
| Answering the Questions | Focus on easier questions first, allocate more time for complex ones |
| Reviewing Your Work | 10-15 minutes at the end |
By organizing your time and staying calm, you’ll increase your chances of performing at your best during the exam.