
Success in math assessments relies heavily on a strong grasp of fundamental principles and problem-solving strategies. As students prepare for their upcoming evaluations, it is essential to focus on understanding key topics, mastering techniques, and practicing effectively to ensure confidence and accuracy under timed conditions.
One of the most effective ways to prepare is by tackling a variety of practice problems that reflect the style and structure of the test. This approach not only helps to reinforce learned material but also familiarizes students with the type of questions they will encounter. It is important to review the thought processes behind each solution, as this will aid in strengthening reasoning skills and quick decision-making.
Utilizing practice resources that include problem sets and solutions is another valuable strategy. This allows learners to check their work and analyze any errors made during the process. By identifying common mistakes and understanding the correct approaches, students can sharpen their ability to answer efficiently and accurately, giving them a competitive edge when the assessment day arrives.
Algebra 1 Final Exam Overview
The upcoming assessment is designed to evaluate students’ understanding of core mathematical principles. It focuses on a range of topics that require critical thinking and the ability to apply concepts effectively. The structure of the test allows students to demonstrate their problem-solving abilities and knowledge in various areas of mathematics.
Key Areas of Focus
For optimal preparation, it is essential to familiarize oneself with the following areas that are commonly tested:
| Topic | Key Concepts |
|---|---|
| Equations | Solving linear and quadratic equations, balancing equations |
| Functions | Identifying functions, function notation, evaluating functions |
| Graphing | Graphing linear and nonlinear functions, slope, intercepts |
| Polynomials | Factoring, simplifying expressions, understanding roots |
| Inequalities | Solving and graphing inequalities, interpreting solutions |
Test Strategy

In order to perform well, students should develop a strong strategy for tackling the test. Reviewing each topic methodically and practicing a variety of problem types will help boost confidence. Additionally, time management is crucial, as it is important to ensure that each section is completed within the allotted time. Practicing past questions can simulate the real test environment and help familiarize students with question formats and difficulty levels.
Key Concepts to Study for the Assessment
To succeed in your upcoming assessment, it is crucial to focus on the core mathematical principles that are most commonly tested. A solid understanding of these fundamental topics will not only help you perform well but also improve your problem-solving skills across different types of questions. Mastering the following areas will ensure you are well-prepared for any challenges that may arise during the test.
Core Topics to Focus On
Make sure to review the following key areas thoroughly:
| Concept | Details |
|---|---|
| Linear Equations | Solve and manipulate equations involving variables, coefficients, and constants. |
| Quadratic Functions | Understand how to solve quadratic equations and graph their corresponding curves. |
| Systems of Equations | Learn to solve systems of equations using substitution or elimination methods. |
| Inequalities | Master solving and graphing inequalities, including linear and compound inequalities. |
| Polynomials | Be comfortable with factoring, expanding, and simplifying polynomial expressions. |
Problem-Solving Techniques
In addition to the topics mentioned above, it is essential to practice specific problem-solving techniques. Becoming proficient in recognizing patterns, simplifying expressions, and applying formulas will help speed up your ability to tackle questions efficiently. Consistent practice through example problems and quizzes will reinforce your understanding and boost your confidence for the actual test.
Understanding Multiple Choice Questions
Being able to effectively navigate questions that provide several potential answers is a valuable skill for any assessment. These questions often test not only your understanding of the material but also your ability to analyze and select the correct response. Recognizing the structure and logic behind such questions can significantly improve your chances of answering them accurately and quickly.
Common Structures of These Questions
Typically, questions that offer a set of possible answers have a specific structure. Understanding how to break down these questions will help you focus on the relevant details and discard any unnecessary information. The key is to carefully read both the question and the options before making a choice.
| Question Type | Description |
|---|---|
| Direct Question | Ask for a specific fact or value based on the material studied. |
| Application Question | Test your ability to apply concepts to solve a problem or scenario. |
| Comparison Question | Require you to compare two or more concepts or ideas and identify the correct relationship. |
| Graph-Based Question | Present a graph or diagram and ask you to interpret or analyze it. |
Effective Strategies for Selecting the Correct Answer
When faced with multiple options, there are several strategies you can use to increase your chances of selecting the correct one. First, eliminate any clearly incorrect choices to narrow down your options. If you are unsure, try to recall related concepts that might help you identify the correct answer. Finally, trust your instincts after reviewing the options, especially when you have a strong understanding of the topic.
Tips for Algebra 1 Exam Success
Succeeding in your assessment requires more than just understanding the material–it also involves effective preparation and strategic thinking. The key to performing well is being proactive, practicing regularly, and managing your time wisely during the test. Here are several tips to help you excel:
- Review Core Concepts: Go over the fundamental topics that are frequently tested, including solving equations, working with functions, and graphing. A strong foundation will give you confidence during the test.
- Practice Regularly: Consistent practice is essential. Use practice questions and quizzes to familiarize yourself with the format and difficulty level of the questions you will encounter.
- Understand the Question Format: Learn the typical structure of problems to anticipate how each question will be presented. This allows you to approach each one efficiently.
- Manage Your Time: During the assessment, pace yourself. Allocate enough time for each section, and avoid spending too much time on any one question.
- Stay Calm and Focused: Stay calm under pressure. Take deep breaths and focus on one question at a time. Avoid second-guessing yourself too often.
Additional Strategies for Success
- Eliminate Incorrect Options: If you’re unsure of the answer, eliminate obviously wrong options first. This increases your chances of selecting the right one.
- Check Your Work: If time permits, go over your answers before submitting the test. Double-check for any mistakes, especially in calculations.
- Ask for Help if Needed: If there are any concepts you’re struggling with, don’t hesitate to seek help from your teacher, tutor, or classmates before the test.
Common Mistakes in Algebra 1 Assessments
During assessments, even the most prepared students can make simple errors that impact their performance. These mistakes often arise from a lack of attention to detail, misapplication of concepts, or rushing through questions. Recognizing and addressing these common pitfalls can significantly improve your score and overall test-taking strategy.
Frequent Errors to Watch For
- Misreading the Question: Many students overlook key words or phrases in the problem, leading to incorrect interpretations of what’s being asked. Carefully read each question and ensure you understand its requirements before selecting an answer.
- Not Following Order of Operations: Forgetting to apply the correct order of operations (PEMDAS) can lead to incorrect calculations. Always work through each problem step-by-step, following the proper sequence.
- Incorrectly Solving for Variables: A common mistake is incorrectly isolating variables when solving equations. Double-check your work to ensure you haven’t missed any steps or made a calculation error.
- Overlooking Negative Signs: Negative signs are easy to miss, but they play a crucial role in many problems. Be particularly careful when adding or subtracting negative numbers.
- Not Checking Work: Failing to review your answers can result in simple mistakes being overlooked. If time permits, always take a moment to check your work before moving on to the next question.
Avoiding These Mistakes

- Slow Down and Read Carefully: Rushing through questions increases the likelihood of errors. Take your time to carefully read each question and check that you understand what is being asked.
- Practice Step-by-Step Solutions: Practice solving problems step-by-step and avoid skipping any intermediate steps. This ensures accuracy and reduces the risk of missing important details.
- Double-Check Your Answers: Whenever possible, review your answers to ensure they make sense. This helps catch any minor mistakes that could otherwise go unnoticed.
Practice Problems to Improve Skills
To master any mathematical topic, consistent practice is essential. Engaging with a variety of problems helps reinforce concepts and develop problem-solving strategies. Regularly tackling problems will not only enhance your ability to apply the material but also build confidence in your skills. Here are some practice problems to improve your understanding and readiness:
- Solving Linear Equations: Solve for x in the following equation: 3x + 5 = 20.
- Graphing Functions: Plot the graph of the function y = 2x – 3. Identify the slope and y-intercept.
- Working with Polynomials: Simplify the expression: (4x^2 + 3x) – (2x^2 – x + 5).
- Factoring Quadratics: Factor the quadratic expression: x^2 + 7x + 12.
- Solving Systems of Equations: Solve the system of equations: x + y = 10 and 2x – y = 3.
- Working with Inequalities: Solve and graph the inequality: 5x – 3 > 7.
By consistently solving these types of problems, you will gain a deeper understanding of key concepts and improve your ability to tackle more complex questions on your assessment.
How to Use Answer Keys Effectively
Answer keys can be a valuable tool in your preparation process, providing insight into correct solutions and offering opportunities for self-correction. However, it’s important to use them strategically to maximize their effectiveness. Simply checking answers without understanding the reasoning behind them can lead to missed learning opportunities. Here are some tips on how to use answer keys to enhance your skills:
Steps for Effective Use of Answer Keys
- Review Your Mistakes: When you check your work, focus on the problems you answered incorrectly. Understand why the correct solution works and how your approach differed.
- Analyze the Solution Process: Don’t just compare your final answer to the key. Examine the steps used to arrive at the solution. Identify any gaps in your understanding and try to replicate the steps in similar problems.
- Practice Concept Reinforcement: If you notice consistent mistakes in a particular topic, revisit that concept. Work through additional problems to reinforce your understanding before moving on.
- Use as a Learning Tool: Instead of relying on the key to simply verify your answers, use it as a guide to learn alternative methods and techniques for solving problems.
Common Pitfalls to Avoid

- Skipping the Process: Avoid the temptation to skip solving a problem altogether if you know you have the answer key. Try to solve problems independently first, using the key only for reference.
- Over-Relying on the Key: Answer keys should be used for learning, not as a shortcut. Constantly using the key without attempting to solve the problems on your own can hinder your progress.
- Ignoring Patterns: Pay attention to recurring mistakes in your work. If you notice a pattern of errors, focus on that specific concept to improve your overall understanding.
By following these guidelines, you can ensure that answer keys become a valuable resource in your study routine, helping you to improve your problem-solving skills and boosting your confidence.
Time Management During the Test

Efficient time management during an assessment is crucial for achieving the best results. Properly allocating your time ensures that you can complete all sections, reduce stress, and avoid rushing through questions. With the right strategy, you can make sure you are giving each problem the attention it deserves while keeping track of the overall time limit.
Strategies for Managing Your Time
- Read Instructions Carefully: Spend a few minutes at the beginning reading the instructions thoroughly. This will help you understand what’s expected and avoid wasting time later on.
- Set a Time Limit for Each Section: Break down the test into smaller sections and allocate a specific amount of time to each one. This will help you stay on track and prevent spending too much time on any single part.
- Prioritize Easier Questions: Start with the questions that you find easier to answer. This will help you build confidence and ensure that you don’t run out of time for the more difficult ones.
- Avoid Getting Stuck: If you encounter a challenging problem, move on and return to it later if time allows. Getting stuck can waste valuable time that could be better spent on other questions.
- Keep Track of Time: Periodically check the clock to ensure you’re staying within your allotted time for each section. This can help you gauge whether you need to speed up or slow down.
Creating a Time Management Plan

| Task | Time Allocation |
|---|---|
| Read instructions and overview | 5 minutes |
| Answer easier questions | 30 minutes |
| Work on challenging problems | 20 minutes |
| Review answers and make corrections | 10 minutes |
By managing your time effectively, you’ll be able to tackle each problem confidently and leave room to double-check your work. Time management is key to success and can make a significant difference in your performance during any test.
Critical Topics in Algebra 1

In any mathematical course, certain concepts form the foundation for mastering more advanced topics. Understanding these key areas ensures a strong grasp of essential principles and prepares you for success in assessments. Focusing on these critical topics will help you navigate through challenges and improve your problem-solving abilities.
Key Areas to Focus On
- Solving Linear Equations: The ability to solve for unknowns in equations is fundamental. Mastering this skill will help you tackle a wide variety of problems effectively.
- Graphing Functions: Being able to graph linear functions and interpret slopes and intercepts is crucial for visualizing relationships between variables.
- Factoring Polynomials: Understanding how to factor expressions helps simplify equations and is an important tool for solving quadratic problems.
- Working with Inequalities: Knowing how to solve and graph inequalities is essential, as they often appear in word problems and real-life applications.
- Systems of Equations: Being able to solve systems of equations, either graphically or algebraically, is vital for handling more complex mathematical scenarios.
- Exponents and Powers: Understanding how to work with exponents, including laws of exponents and scientific notation, is essential for solving problems involving large numbers or formulas.
Recommended Practice Areas

- Word Problems: These test your ability to translate real-world situations into mathematical equations. Practice setting up and solving these types of problems to improve your understanding.
- Quadratic Equations: Be sure to practice solving quadratics by factoring, completing the square, and using the quadratic formula.
- Rational Expressions: Working with fractions that involve variables is another critical skill. Simplifying, multiplying, and dividing rational expressions are key areas to focus on.
By mastering these essential topics, you’ll be well-equipped to solve a broad range of problems and demonstrate your mathematical proficiency in assessments.
Interpreting Algebraic Expressions Correctly
Understanding how to read and interpret mathematical expressions is crucial for solving problems accurately. When you encounter an algebraic statement, recognizing the relationship between variables and constants is essential to make the correct calculations. Misinterpreting an expression can lead to errors that affect the entire solution, so developing a strong skill in analyzing these statements is key to success.
Key Steps to Interpret Expressions
- Identify Operators: The first step is to identify the operations involved, such as addition, subtraction, multiplication, or division. These operations determine how the numbers and variables relate to each other.
- Understand Parentheses: Pay close attention to parentheses or other grouping symbols, as they indicate which operations should be performed first. This is crucial for ensuring the correct order of operations.
- Recognize Variables and Constants: Distinguish between variables (symbols representing unknown values) and constants (fixed numbers). Understanding this difference is fundamental for solving expressions.
- Translate Word Problems: Practice translating verbal descriptions into mathematical expressions. This skill helps you understand real-life situations and convert them into solvable equations.
Common Pitfalls to Avoid
- Misinterpreting Negative Signs: Be careful when working with negative numbers, especially when they appear next to parentheses. Failing to correctly interpret negative signs can lead to errors in the final result.
- Forgetting the Order of Operations: Always remember the correct sequence of operations (PEMDAS/BODMAS) to ensure you’re solving expressions in the right order.
- Overlooking Exponents: Exponents often appear in complex expressions and can significantly alter the outcome. Be sure to treat them carefully when they are present.
By improving your ability to correctly interpret algebraic statements, you’ll enhance your problem-solving skills and avoid common mistakes that can affect your results.
Strategies for Solving Word Problems
Word problems are often seen as one of the most challenging parts of mathematics, as they require not only mathematical knowledge but also the ability to interpret real-world situations. The key to solving these problems effectively lies in translating the given information into a mathematical form. By following a structured approach, you can break down the problem and solve it step by step.
Step-by-Step Approach
- Read the Problem Carefully: Begin by reading the problem thoroughly to understand what is being asked. Pay close attention to the details and underline or highlight key pieces of information.
- Identify the Unknowns: Determine what the problem is asking you to find. These are the unknowns that will become the variables in your equation.
- Translate Words into Math: Convert the words in the problem into a mathematical expression. Look for keywords such as “total,” “difference,” “product,” or “quotient” that indicate operations like addition, subtraction, multiplication, or division.
- Set Up an Equation: Based on the translation, write an equation that represents the relationships described in the problem. Ensure that all known quantities are included.
- Solve the Equation: Use the appropriate mathematical techniques to solve the equation. Be sure to follow the order of operations and check your work as you go.
- Interpret the Solution: After finding the solution, make sure to answer the specific question asked in the problem. Verify that your answer makes sense in the context of the problem.
Tips for Success

- Practice with Various Problems: The more word problems you solve, the more familiar you will become with different problem types. This practice will help you recognize patterns and choose the right approach.
- Use Diagrams or Charts: For problems involving measurements or comparisons, drawing a diagram or creating a table can help visualize the relationships between quantities.
- Check Units and Dimensions: Always ensure that your solution has the correct units. Converting units, when necessary, is an important step in maintaining accuracy.
By applying these strategies, you can approach word problems with confidence and solve them more efficiently. Developing these skills will help improve your overall problem-solving abilities and contribute to your success in mathematical tasks.
Mastering Equations and Inequalities
Understanding how to solve and manipulate equations and inequalities is a fundamental skill in mathematics. These concepts form the foundation for many more advanced topics and are essential for problem-solving in various contexts. The key to mastering them is developing a clear approach to simplify, solve, and interpret the results correctly.
Solving Equations Step by Step

To solve an equation, the goal is to find the value of the unknown variable that makes the equation true. This process typically involves isolating the variable on one side of the equation through a series of logical steps:
- Combine Like Terms: Begin by simplifying both sides of the equation. This often involves adding or subtracting like terms.
- Isolate the Variable: Use addition, subtraction, multiplication, or division to move all terms involving the variable to one side of the equation.
- Solve for the Variable: Once the variable is isolated, perform any remaining operations to solve for its value.
- Check the Solution: Always substitute the solution back into the original equation to verify that it satisfies the equation.
Understanding and Solving Inequalities
Inequalities are similar to equations, but instead of finding a specific value, the goal is to find a range of values that satisfy the inequality. Solving inequalities involves many of the same steps as solving equations, but with a few important differences:
- Reverse the Inequality Sign: When multiplying or dividing both sides of an inequality by a negative number, the inequality sign must be reversed.
- Graph the Solution: Inequalities often have multiple solutions, which can be represented on a number line. Understanding how to graph these solutions helps in visualizing the possible outcomes.
- Check the Boundary: Make sure to check whether the boundary values (such as those involving “greater than” or “less than or equal to”) are included in the solution set.
By consistently practicing these techniques, you can gain a deep understanding of how to manipulate both equations and inequalities. This foundational knowledge will significantly improve your ability to solve complex problems efficiently and accurately.
Factoring and Simplifying Algebraic Expressions
Breaking down complex expressions into simpler components is a key skill in mathematics. Factoring and simplifying are essential tools for solving problems efficiently. By recognizing patterns and applying basic rules, you can transform expressions into more manageable forms, making it easier to solve for unknowns or simplify the problem at hand.
Understanding Factoring Techniques
Factoring involves rewriting an expression as a product of simpler expressions. This technique is particularly useful when solving equations or simplifying complex problems. Some common methods of factoring include:
- Greatest Common Factor (GCF): Find the largest factor that all terms in the expression share and factor it out.
- Factoring by Grouping: Group terms in a way that makes it easier to factor out common binomials.
- Difference of Squares: Recognize when an expression is the difference between two perfect squares and apply the formula a² – b² = (a – b)(a + b).
- Trinomial Factoring: When an expression is a trinomial, factor it into two binomials using methods such as trial and error or the AC method.
Simplifying Expressions Effectively
Simplifying algebraic expressions helps to reduce them to their most basic form, making calculations easier. To simplify an expression:
- Combine Like Terms: Identify terms that have the same variable raised to the same power and combine them by adding or subtracting.
- Apply the Distributive Property: Use a(b + c) = ab + ac to remove parentheses and simplify expressions.
- Cancel Common Factors: In fractions, look for common factors in the numerator and denominator that can be canceled out.
Mastering the art of factoring and simplifying will not only streamline solving problems but also help in understanding more complex mathematical concepts. With regular practice, you can become proficient in recognizing patterns and applying the right techniques to solve problems more efficiently.
Handling Linear Functions with Confidence
Understanding and working with linear functions is a fundamental aspect of solving mathematical problems. A linear function represents a relationship between two variables where the rate of change remains constant. This makes them predictable and relatively easy to work with once you master the basic principles. Whether you’re graphing, solving equations, or analyzing trends, mastering linear functions will make your problem-solving process more efficient and intuitive.
Key Concepts for Linear Functions
To handle linear functions confidently, it’s important to understand the core concepts that define them. Some essential points to keep in mind include:
- Slope: The slope of a line measures its steepness and is calculated as the ratio of the change in the y-values to the change in the x-values. It is often represented as m in the equation of a line.
- Y-Intercept: The y-intercept is the point where the line crosses the y-axis. This is a key part of the equation and is represented as b in the slope-intercept form, y = mx + b.
- Equation of a Line: The general form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept. Understanding how to write and manipulate this equation is crucial.
Practical Tips for Solving Problems
Here are some tips to help you tackle linear functions effectively:
- Graphing: When graphing a linear function, always start by plotting the y-intercept, then use the slope to find another point on the line. Draw a straight line through these points.
- Solving for Variables: To solve linear equations, isolate the variable by performing inverse operations. Be sure to check your work by substituting the solution back into the original equation.
- Understanding Proportionality: Linear functions often represent proportional relationships. If you can recognize proportionality, you can easily write the equation of the line and solve related problems.
By practicing these concepts and strategies, you’ll be able to approach linear functions with confidence, making it easier to solve problems quickly and accurately. Remember, the more you practice, the more intuitive working with linear relationships will become.
Graphing Techniques for Algebra 1
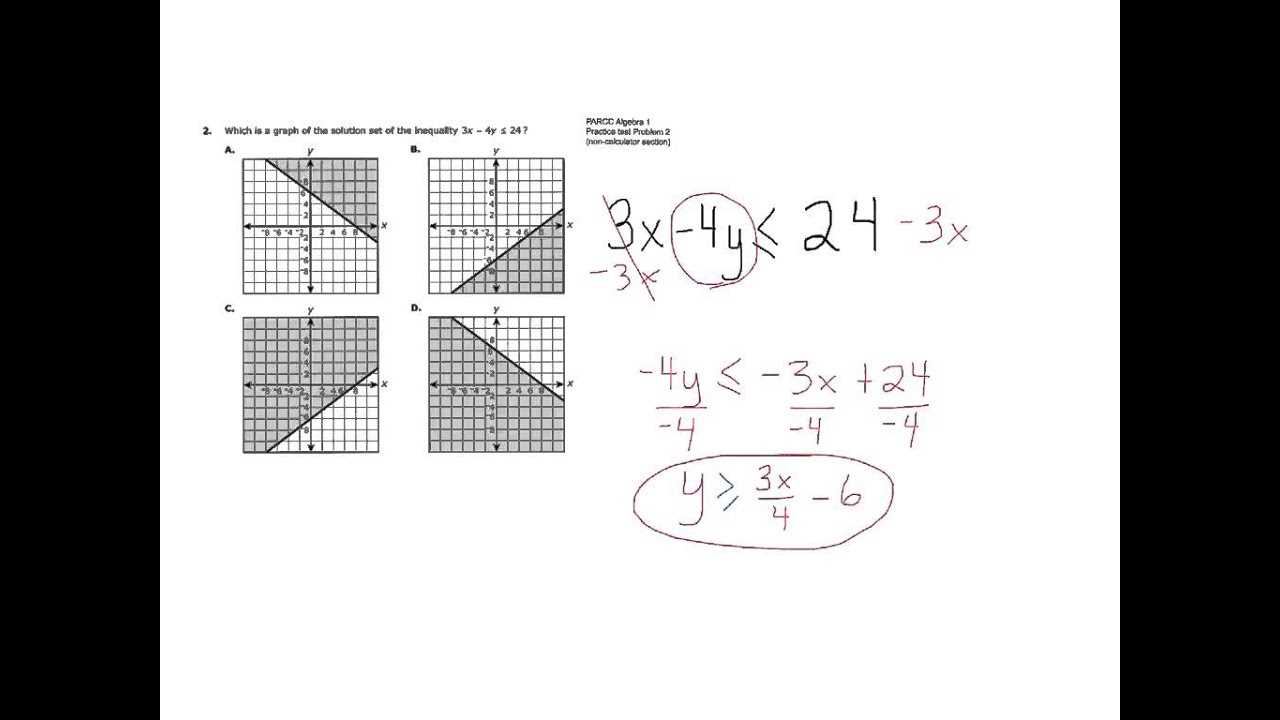
Graphing is an essential skill when working with mathematical relationships, as it provides a visual representation of equations and helps in understanding the behavior of different functions. Whether you’re dealing with linear equations, quadratic functions, or inequalities, mastering graphing techniques will make it easier to interpret and solve problems efficiently. Knowing how to plot points, draw lines, and recognize key features on a graph is critical for success.
Basic Steps for Graphing Linear Equations
For linear relationships, the graph is a straight line, and understanding how to plot it accurately is key. Follow these basic steps:
- Identify the Slope and Y-Intercept: The equation of a line is typically written in the slope-intercept form y = mx + b, where m is the slope, and b is the y-intercept. These two values give you essential information to plot the line.
- Plot the Y-Intercept: Start by plotting the point on the y-axis where the line crosses, which is represented by the value of b.
- Use the Slope: From the y-intercept, use the slope m to find a second point. The slope is a ratio of the change in y over the change in x, so move up/down and left/right accordingly. Plot this second point.
- Draw the Line: Once two points are plotted, draw a straight line through them. This line represents the solution to the equation.
Graphing Inequalities
Graphing inequalities requires a slightly different approach, as the solutions are often represented by shaded regions instead of a single line. Here’s how to graph inequalities:
- Graph the Boundary Line: First, graph the boundary line as you would for an equation. If the inequality includes > or < (not equal to), use a dashed line to indicate that points on the line are not part of the solution.
- Shade the Region: After graphing the boundary, determine which side of the line contains the solutions. Use a test point (such as (0,0)) to check if the point satisfies the inequality. Shade the side that includes the test point if it holds true.
By following these techniques, you’ll be able to accurately graph both equations and inequalities, providing you with a clear visual of the solution sets and helping you solve problems more effectively.
Reviewing Algebra 1 Answer Explanations
Understanding the reasoning behind solutions is just as important as obtaining the correct result. When reviewing your work, it is essential to not only check whether your answers are accurate but also comprehend the steps that lead to those conclusions. This helps strengthen problem-solving skills and ensures that you can apply the techniques effectively in future problems. Analyzing the logic behind each step will deepen your understanding and enhance your ability to approach similar challenges with confidence.
Breaking Down the Steps
When reviewing solutions, focus on each step taken to solve the problem. Ensure that the correct methods were used and that every calculation is accounted for. Here are some key points to consider:
- Identifying Key Information: Before solving, make sure that you’ve identified all the relevant information in the problem. This could include coefficients, constants, or specific instructions that guide how to approach the problem.
- Applying the Right Method: Double-check that the method you used (e.g., solving equations, simplifying expressions) is the appropriate one for the problem type. Some problems may require factoring, while others might involve applying formulas or properties.
- Verifying the Process: Go through each step again to ensure no mistakes were made, especially in arithmetic operations or the use of properties. It’s easy to overlook small errors that can lead to incorrect answers.
Common Mistakes to Avoid

During review, it’s helpful to recognize common mistakes that students tend to make. By knowing what to look for, you can avoid these pitfalls and improve your accuracy:
- Skipping Steps: While it may seem faster to skip steps, this can lead to errors or confusion later on. Write down every step to maintain clarity and ensure you don’t miss anything crucial.
- Incorrect Sign Handling: Watch out for sign errors, especially when multiplying or dividing negative numbers. These mistakes can significantly affect the final answer.
- Misinterpreting the Question: Sometimes, the solution may be correct, but the interpretation of the problem might have been wrong. Always take a moment to read the problem carefully and make sure you understand exactly what is being asked.
By reviewing each solution thoroughly and understanding the rationale behind the methods used, you’ll improve both your accuracy and efficiency in solving problems. This practice not only prepares you for future challenges but also reinforces your overall understanding of the subject.