Preparing for a significant assessment can feel overwhelming, but with the right strategies and focus, you can tackle the challenges ahead. This section is designed to provide a structured approach to mastering key concepts, ensuring you’re ready to perform at your best. By breaking down the core material and addressing common problem areas, you’ll gain confidence and clarity.
We will explore various mathematical principles, going through each topic systematically to help you understand both the basics and the more complex ideas. Alongside the explanations, you will find step-by-step solutions and detailed insights to reinforce your learning. Whether you’re revisiting familiar concepts or tackling more challenging problems, this guide will serve as an essential resource for your test preparation.
Essential Topics for Test Preparation
To perform well on the upcoming assessment, it’s crucial to focus on key areas that are frequently tested. Understanding the foundational concepts will not only help you solve problems efficiently but also allow you to approach more complex scenarios with confidence. This section highlights the core topics that you should prioritize as you prepare.
Equations and Functions
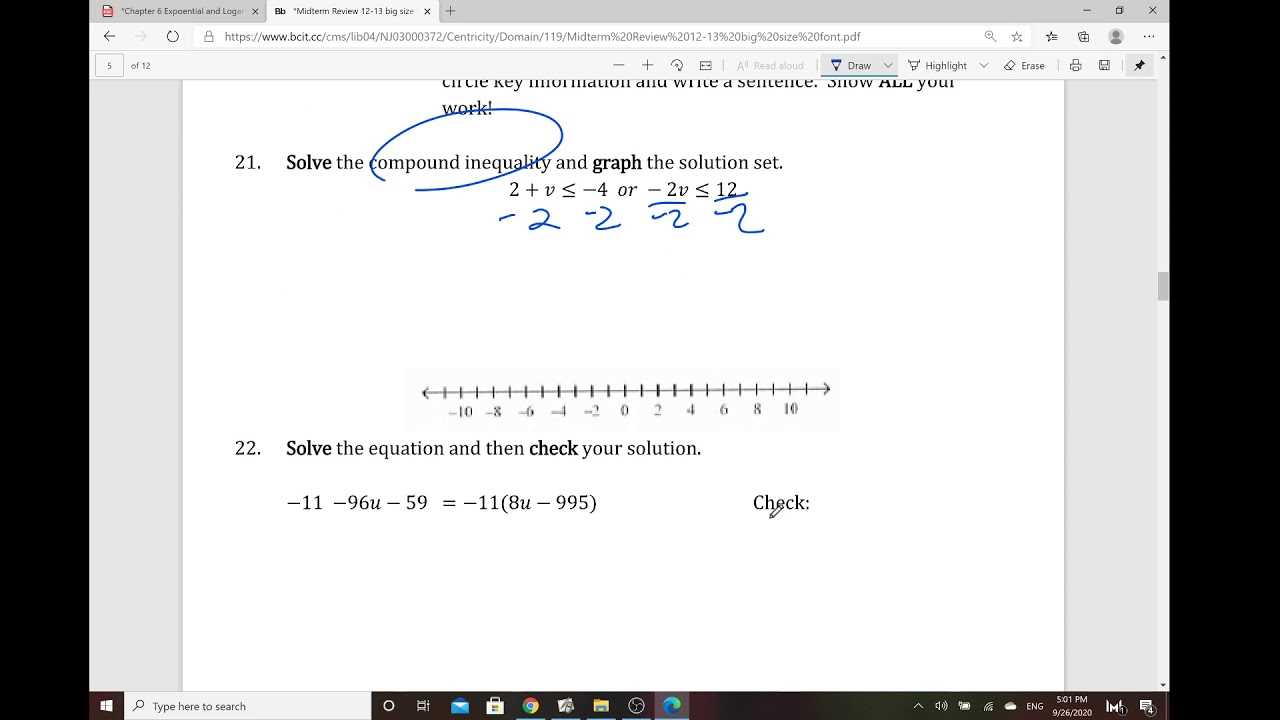
One of the primary skills you’ll need to master is solving various types of equations. This includes linear equations, systems of equations, and inequalities. Being able to manipulate and solve for unknowns is essential in a wide range of problems. Additionally, understanding functions, their graphs, and how to interpret them will be central to many questions.
Factoring and Polynomial Expressions
Another crucial area is working with polynomials. You’ll need to be comfortable with factoring techniques, including factoring quadratics and higher-degree expressions. Recognizing patterns and applying appropriate methods to simplify expressions will significantly enhance your problem-solving abilities during the test.
Review of Linear Equations and Solutions
Solving equations where the highest power of the variable is one forms the foundation of many mathematical concepts. Mastering the techniques to isolate the variable and find its value is essential for solving a wide range of problems. This section will cover the methods and strategies needed to approach these types of problems effectively.
Solving Simple Linear Equations
One of the first steps in this process is solving basic equations, such as x + 5 = 12. To find the value of x, you must perform inverse operations to isolate the variable. These equations often require adding, subtracting, multiplying, or dividing both sides to achieve the solution.
Working with Systems of Equations
In some cases, you will encounter multiple equations that share variables. These are called systems of equations, and they can be solved using various methods, such as substitution or elimination. Understanding how to manipulate and combine these equations will allow you to find the values of the variables that satisfy all given conditions.
Understanding Quadratic Functions and Graphing
Quadratic expressions represent a significant category of mathematical functions, commonly seen in various problem-solving scenarios. These functions can be graphed as curves and have distinct features that help in understanding their behavior. This section will break down how to analyze and graph these functions, focusing on their key characteristics and methods for plotting them on a coordinate plane.
Key Characteristics of Quadratic Functions
One of the most important aspects of a quadratic equation is its shape, which forms a parabola. The equation typically takes the form of y = ax² + bx + c, where the values of a, b, and c determine the position and orientation of the graph. The vertex, the highest or lowest point of the parabola, and the axis of symmetry, a vertical line that divides the graph into two mirror-image halves, are critical in understanding how the graph behaves.
Graphing a Quadratic Function
To graph a quadratic equation, start by calculating the vertex and plotting it on the coordinate system. Next, determine whether the parabola opens upwards or downwards based on the value of a. Once the vertex is plotted, additional points can be found by selecting various values for x and calculating the corresponding y values. The table below demonstrates this process for the equation y = x² – 4x + 3:
| x | y = x² – 4x + 3 |
|---|---|
| -1 | 8 |
| 0 | 3 |
| 1 | 0 |
| 2 | -1 |
| 3 | 0 |
Once sufficient points are plotted, connect them to form the curve of the parabola. The graph will help visually represent the relationship between the variables and provide insight into the behavior of the function.
Key Concepts in Polynomial Expressions
Polynomials are fundamental mathematical expressions that involve multiple terms, each consisting of a variable raised to a certain power. Understanding these expressions is essential for solving more complex equations and problems. In this section, we will focus on the important ideas related to working with polynomials, from basic operations to advanced concepts.
Types of Polynomial Terms
Polynomials consist of different terms, each having a coefficient and an exponent. It’s important to recognize the different forms these terms can take. Here are the common types:
- Monomials – Polynomials with a single term, such as 3x or 5y².
- Binomials – Polynomials with two terms, such as x + 2 or 4a – 7b.
- Trinomials – Polynomials with three terms, like x² + 5x + 6.
- Multinomial expressions – Polynomials with more than three terms.
Operations on Polynomials
Polynomials can be added, subtracted, multiplied, and divided. Below are the key operations you’ll need to master:
- Addition: Combine like terms by adding the coefficients of the same variable powers.
- Subtraction: Subtract the coefficients of like terms.
- Multiplication: Multiply each term in the first polynomial by every term in the second polynomial.
- Division: Use long division or synthetic division to divide one polynomial by another.
Mastering these operations will help you manipulate polynomial expressions and solve equations efficiently. Understanding the structure and behavior of polynomials is a critical step toward mastering higher-level math concepts.
Solving Systems of Linear Equations
When dealing with multiple unknowns, solving systems of linear equations allows you to find values that satisfy all given conditions simultaneously. These systems consist of two or more linear equations that share common variables. In this section, we will explore different methods for solving these systems and how to approach them effectively.
Methods for Solving Systems
There are several ways to solve a system of linear equations. The most common methods include substitution, elimination, and graphical solutions. Each method has its advantages depending on the structure of the equations and the complexity of the problem.
- Substitution: Solve one equation for one variable and substitute that expression into the other equation(s) to find the values of the remaining variables.
- Elimination: Add or subtract the equations to eliminate one variable, making it easier to solve for the other variable(s).
- Graphical Method: Plot both equations on a coordinate plane and identify the point(s) where the lines intersect. This point represents the solution to the system.
Example of Solving by Substitution
Consider the following system:
- 2x + y = 8
- x – y = 2
To solve by substitution, solve the second equation for x: x = y + 2. Then, substitute this into the first equation:
2(y + 2) + y = 8
Simplify and solve for y, then substitute the value of y back into the expression for x to find the solution.
By using these methods, you can solve systems of equations efficiently and accurately, ensuring that all variables are correctly determined.
Factoring Techniques for Algebraic Expressions
Factoring is a crucial skill in simplifying expressions and solving equations. It involves rewriting an expression as a product of its factors. Mastering different factoring techniques can make it easier to solve complex problems and simplify expressions. In this section, we’ll explore various methods for factoring algebraic expressions and when to apply them effectively.
The most common factoring methods include:
- Factoring out the Greatest Common Factor (GCF): Identify the largest common factor of all terms in the expression and factor it out. This simplifies the expression and makes further factoring easier.
- Factoring Trinomials: For quadratic expressions of the form ax² + bx + c, find two numbers that multiply to ac and add up to b. These values can be used to split the middle term, allowing you to factor by grouping.
- Difference of Squares: Expressions of the form a² – b² can be factored as (a + b)(a – b). This is a special case of factoring that simplifies the process significantly.
- Perfect Square Trinomial: Trinomials like a² + 2ab + b² can be factored as (a + b)². Recognizing these patterns helps to speed up the factoring process.
By mastering these techniques, you can easily break down complex expressions and solve problems more efficiently, improving your understanding of mathematical concepts.
Rational Expressions and Their Simplification
Rational expressions are mathematical fractions where both the numerator and the denominator are polynomials. Simplifying these expressions is essential for making them more manageable and easier to work with in equations. In this section, we will explore how to simplify rational expressions by factoring and canceling common terms.
Steps to Simplify Rational Expressions
To simplify a rational expression, you need to factor both the numerator and the denominator completely, then cancel out any common factors. The process can be broken down into the following steps:
- Factor the numerator and denominator: Start by factoring both parts of the fraction as completely as possible.
- Cancel common factors: If there are any factors that appear in both the numerator and denominator, cancel them out.
- Check for restrictions: Ensure that the values that would make the denominator zero are excluded from the solution set.
Example of Simplifying a Rational Expression
Consider the rational expression:
(frac{2x^2 + 6x}{4x^2 + 12x})
First, factor both the numerator and denominator:
| Expression | Factored Form |
|---|---|
| Numerator | 2x(x + 3) |
| Denominator | 4x(x + 3) |
Next, cancel the common factor of (x(x + 3)) from both the numerator and the denominator:
(frac{2x(x + 3)}{4x(x + 3)} = frac{2}{4} = frac{1}{2})
After simplification, the expression reduces to (frac{1}{2}), demonstrating how factoring and canceling common factors can simplify the original rational expression.
Working with Exponents and Powers
Understanding exponents and powers is crucial in simplifying expressions and solving mathematical problems efficiently. Exponents represent repeated multiplication, while powers provide a way to express large numbers more compactly. This section will explore key rules and methods for manipulating powers and exponents in various expressions.
Key Rules for Exponents
There are several fundamental rules that guide the operations with exponents. These rules help simplify expressions and make calculations more manageable:
- Product Rule: When multiplying two terms with the same base, add the exponents. For example, (a^m cdot a^n = a^{m+n}).
- Quotient Rule: When dividing terms with the same base, subtract the exponents. For example, (frac{a^m}{a^n} = a^{m-n}).
- Power of a Power: To raise a power to another power, multiply the exponents. For example, ((a^m)^n = a^{m cdot n}).
- Power of a Product: When raising a product to a power, apply the exponent to each factor. For example, ((ab)^n = a^n cdot b^n).
- Negative Exponent: A negative exponent represents the reciprocal of the base raised to the positive exponent. For example, (a^{-n} = frac{1}{a^n}).
- Zero Exponent: Any non-zero base raised to the zero power is equal to 1. For example, (a^0 = 1) (where (a neq 0)).
Example: Simplifying Expressions
Let’s simplify the expression ( frac{2x^3 cdot y^4}{x^2 cdot y} ) using the exponent rules:
- First, apply the quotient rule to the terms with the same base:
- For (x), subtract the exponents: (x^{3-2} = x^1).
- For (y), subtract the exponents: (y^{4-1} = y^3).
- The simplified expression is: ( 2x cdot y^3 ).
By applying the exponent rules, you can easily simplify expressions and solve complex problems more efficiently.
Radicals and Square Root Operations
Working with square roots and radicals is a key part of simplifying expressions and solving equations. These operations involve finding numbers that, when multiplied by themselves, yield the original value. Mastering the rules for handling these operations helps simplify more complex problems and enables efficient solutions. In this section, we will explore the essential concepts and techniques for manipulating square roots and other radical expressions.
One of the most common operations involving radicals is simplifying square roots. For example, the square root of a number represents the value that, when squared, equals the original number. For instance, ( sqrt{25} = 5 ), because ( 5^2 = 25 ). Simplifying expressions that contain square roots or other radicals involves reducing them to their simplest form.
Simplifying Square Roots
To simplify square roots, identify perfect squares within the radical. For example:
- Example 1: ( sqrt{50} ) can be simplified as ( sqrt{25 cdot 2} = sqrt{25} cdot sqrt{2} = 5sqrt{2} ).
- Example 2: ( sqrt{72} ) simplifies to ( sqrt{36 cdot 2} = sqrt{36} cdot sqrt{2} = 6sqrt{2} ).
Operations with Radicals
When performing operations with radicals, such as addition, subtraction, multiplication, and division, it’s important to follow certain rules:
- Adding or subtracting radicals: You can only combine radicals with the same radicand. For example, ( 2sqrt{3} + 5sqrt{3} = 7sqrt{3} ), but ( 2sqrt{3} + 5sqrt{2} ) cannot be simplified further.
- Multiplying radicals: When multiplying radicals, multiply the numbers under the radicals. For example, ( sqrt{3} cdot sqrt{12} = sqrt{36} = 6 ).
- Dividing radicals: To divide radicals, divide the numbers under the radicals. For example, ( frac{sqrt{12}}{sqrt{3}} = sqrt{4} = 2 ).
By understanding these techniques, you can simplify expressions involving square roots and perform more advanced operations involving radicals with ease.
Solving Word Problems in Algebra

Word problems can be one of the most challenging aspects of mathematics, as they require translating real-life situations into mathematical expressions. By breaking down the information provided and identifying key elements, you can convert the problem into an equation that can be solved. The ability to understand and set up equations from verbal descriptions is a critical skill for solving these types of problems effectively.
Step-by-Step Approach
To solve word problems, follow these steps:
- Read the problem carefully: Understand what the question is asking and identify the given information. Pay attention to units and relationships between quantities.
- Define variables: Assign variables to unknowns. For example, let ( x ) represent the number of apples, or ( y ) the total cost.
- Set up an equation: Translate the problem into a mathematical expression using the relationships described in the problem. Use arithmetic operations and variables.
- Solve the equation: Use appropriate methods such as addition, subtraction, multiplication, or division to find the value of the variable(s).
- Check your solution: Substitute the value of the variable back into the problem to ensure that it makes sense and satisfies the conditions.
Example Problem
Consider this example:
“A bookstore sells pencils at $2 each and erasers at $3 each. If a customer buys 5 pencils and some erasers for a total of $21, how many erasers did they purchase?”
First, let ( x ) represent the number of erasers purchased. The equation based on the given information would be:
( 5 cdot 2 + 3x = 21 )
Solving the equation:
- First, simplify: ( 10 + 3x = 21 )
- Next, subtract 10 from both sides: ( 3x = 11 )
- Then, divide both sides by 3: ( x = frac{11}{3} )
In this case, the number of erasers purchased is ( frac{11}{3} ), which is not a whole number. Thus, the question might need to be revisited, or the problem could have additional details not included in the initial setup.
By following the steps outlined, you can approach any word problem in a structured and systematic way, ensuring that the solution is both accurate and reasonable.
Important Formulas to Memorize
Having a solid grasp of key mathematical formulas is essential for solving problems efficiently. These formulas serve as the foundation for many concepts and help streamline the problem-solving process. Memorizing the most commonly used formulas allows you to quickly recognize patterns and apply the right method to reach a solution.
Essential Arithmetic and Algebraic Formulas
Here are some of the most important formulas to remember:
- Distributive Property: ( a(b + c) = ab + ac )
- Area of a Rectangle: ( A = l times w ), where ( l ) is the length and ( w ) is the width.
- Quadratic Formula: ( x = frac{-b pm sqrt{b^2 – 4ac}}{2a} ), used to solve quadratic equations ( ax^2 + bx + c = 0 ).
- Slope Formula: ( m = frac{y_2 – y_1}{x_2 – x_1} ), used to calculate the slope between two points ( (x_1, y_1) ) and ( (x_2, y_2) ).
Key Geometry and Exponent Rules
In addition to the basic formulas, some fundamental rules are critical for understanding geometry and working with powers:
- Pythagorean Theorem: ( a^2 + b^2 = c^2 ), where ( a ) and ( b ) are the legs of a right triangle, and ( c ) is the hypotenuse.
- Exponent Rule: ( x^a times x^b = x^{a+b} ), used to combine terms with the same base.
- Power of a Power: ( (x^a)^b = x^{a times b} ), used to simplify expressions with exponents.
- Volume of a Cube: ( V = s^3 ), where ( s ) is the length of a side of the cube.
By committing these essential formulas to memory, you can tackle a wide range of problems more effectively and confidently. Having them readily available allows for faster calculations and less reliance on external resources, improving both speed and accuracy in problem-solving.
Algebraic Manipulation and Techniques
Mastering the art of simplifying expressions and solving equations is key to understanding and applying mathematical principles. Manipulating terms and transforming equations efficiently allows for quick problem-solving. By utilizing certain techniques, complex problems become more manageable and lead to straightforward solutions.
Key Methods of Simplification
Several fundamental strategies are used to simplify algebraic expressions and solve equations:
- Combining Like Terms: This technique involves adding or subtracting terms that have the same variable and exponent. For example, ( 3x + 2x = 5x ).
- Distributive Property: Use this property to remove parentheses by multiplying the outer term by each term inside the parentheses. For example, ( 3(x + 4) = 3x + 12 ).
- Factoring: Break down expressions into simpler components, such as factoring ( x^2 – 9 ) into ( (x – 3)(x + 3) ).
- Cross-multiplication: A useful method when solving proportions, where you multiply diagonally to eliminate fractions. For example, ( frac{a}{b} = frac{c}{d} ) becomes ( a times d = b times c ).
Advanced Techniques for Solving Equations
When working with more complex equations, certain techniques become especially useful for finding solutions:
- Substitution: Replace one variable with an expression that contains another variable. This is commonly used in systems of equations.
- Elimination: Add or subtract equations to eliminate one of the variables, making it easier to solve for the remaining variable.
- Completing the Square: A technique often used to solve quadratic equations by converting them into perfect square trinomials. For example, ( x^2 + 6x = 7 ) becomes ( (x + 3)^2 = 16 ).
- Using the Quadratic Formula: For quadratic equations, the quadratic formula ( x = frac{-b pm sqrt{b^2 – 4ac}}{2a} ) allows for the direct calculation of roots.
By applying these techniques, solving equations and simplifying expressions becomes much more systematic. Mastery of these methods not only saves time but also enhances problem-solving abilities across various mathematical challenges.
Graphing and Analyzing Functions
Understanding how to graph and interpret mathematical functions is a critical skill in solving various types of equations. The ability to represent relationships between variables visually not only helps in solving problems but also aids in recognizing patterns and behaviors of different equations. Analyzing the shape, slope, and key points on a graph is essential for drawing accurate conclusions.
Key Elements of a Function’s Graph
When graphing a function, there are several important components to consider:
- Intercepts: The points where the graph crosses the axes. The x-intercept occurs when the output is zero, and the y-intercept occurs when the input is zero.
- Slope: The steepness or incline of the graph, which can reveal how the values of the variables change in relation to one another.
- Vertex: For parabolas and other quadratic functions, the vertex represents the highest or lowest point on the curve.
- Asymptotes: Lines that the graph approaches but never touches, often seen in rational functions or hyperbolas.
Understanding and Using a Table for Graphing
A table of values is a useful tool for plotting points on a graph. It helps to identify key points and visualize the graph accurately. Below is an example of a table for a linear function:
| x | y |
|---|---|
| -2 | 4 |
| -1 | 2 |
| 0 | 0 |
| 1 | -2 |
| 2 | -4 |
This table shows the corresponding values of x and y, which can be plotted to create a straight line. By connecting the points, one can easily visualize the relationship between the variables.
Graphing functions is an essential skill for solving mathematical problems, allowing for both quick insight and a deeper understanding of how different equations behave under various conditions. Mastery of this process enhances problem-solving capabilities across a wide range of topics.
Tips for Effective Test Preparation
Preparing for an upcoming exam requires not just reviewing materials, but also adopting strategic methods to ensure comprehensive understanding and retention of concepts. The goal is to maximize your study efforts, manage time effectively, and approach the test with confidence. Using a structured plan and focused study techniques can make all the difference in your performance.
Create a Study Schedule
One of the most important steps in preparing for any exam is setting up a structured study schedule. It helps you allocate time for each topic and ensures you cover everything that will be on the test. Break down the content into smaller, manageable sections and dedicate specific days to review each one. Prioritize areas where you feel less confident and gradually build up to more challenging topics.
- Start Early: Don’t wait until the last minute. Begin your preparations well in advance to avoid unnecessary stress.
- Set Realistic Goals: Establish clear, achievable targets for each study session, such as mastering a particular concept or solving a set number of problems.
- Balance Your Time: Include time for both active learning (e.g., solving problems) and passive review (e.g., reading notes).
Practice Regularly and Test Yourself
Regular practice is essential for reinforcing the material you’ve learned. Work through practice problems, sample questions, and past exams to get comfortable with the types of questions you might encounter. Self-testing allows you to assess your understanding, pinpoint weak areas, and build your problem-solving skills.
- Use Practice Exams: Taking full-length practice tests under timed conditions will help you get accustomed to the exam format and manage your time more effectively.
- Review Mistakes: Carefully go over any errors you make while practicing. Understanding where you went wrong is crucial for improvement.
- Mix Up Topics: Rather than focusing on one topic at a time, mix different concepts together in your practice sessions to simulate the actual test environment.
By following these strategies, you will be better prepared to tackle the exam confidently and efficiently. Consistent practice, proper time management, and a structured approach will help you perform at your best.
Common Mistakes to Avoid During the Exam
When taking any test, it’s easy to make mistakes under pressure. Being aware of common pitfalls can help you avoid them and ensure that you perform your best. By staying mindful of certain missteps, you can maintain focus, manage your time effectively, and reduce the likelihood of errors that could cost you valuable points.
Rushing Through Questions
One of the biggest mistakes students make during an exam is rushing through questions. In the effort to finish quickly, it’s easy to overlook important details or skip steps in solving problems. Taking your time to read each question carefully and ensuring that your work is complete can help you avoid careless mistakes.
- Read the Instructions: Always carefully read the instructions for each question to understand exactly what is being asked.
- Check Your Work: If time allows, double-check your answers before submitting your test to catch any simple mistakes.
Mismanaging Time
Time management is crucial to completing an exam successfully. Spending too much time on one question while neglecting others can leave you with an unfinished test. It’s important to pace yourself and move on when you’re stuck, coming back to difficult questions if there is time left.
- Prioritize Easy Questions: Start by answering the questions that you find easiest. This helps build confidence and ensures you get those points.
- Set Time Limits: Try to allocate a specific amount of time to each question or section to avoid spending too long on any one part.
Forgetting Key Formulas
Another common issue is forgetting important formulas or concepts that are necessary to solve problems. While studying, make sure to review key formulas and methods, and be sure to keep a list handy during the test if it’s allowed. If not, try to mentally recall the most important ones before starting the exam.
| Formula | Application |
|---|---|
| Quadratic Formula | Solving quadratic equations |
| Distributive Property | Expanding expressions |
| FOIL Method | Multiplying binomials |
By recognizing these common mistakes, you can better prepare yourself to approach the exam calmly and efficiently, increasing your chances of success.
Answer Key and Detailed Explanations
Understanding the solutions to problems is crucial for reinforcing your comprehension of mathematical concepts. This section provides clear solutions along with step-by-step explanations for each problem, offering insight into the problem-solving process and helping you grasp key techniques. By studying the methods used to arrive at the correct results, you can develop a deeper understanding and avoid common mistakes in the future.
Example 1: Solving a Linear Equation
Consider the equation:
3x + 5 = 20
To solve for x, follow these steps:
- Start by subtracting 5 from both sides: 3x = 15.
- Next, divide both sides by 3 to isolate x: x = 5.
The solution is x = 5. This demonstrates the basic technique for solving a simple linear equation by isolating the variable.
Example 2: Factoring a Quadratic Expression
Now, let’s factor the quadratic expression:
x² + 5x + 6
To factor this expression, follow these steps:
- Look for two numbers that multiply to 6 and add up to 5. These numbers are 2 and 3.
- Rewrite the expression as (x + 2)(x + 3).
The factored form of the expression is (x + 2)(x + 3). Factoring quadratics involves finding two binomials whose product is equal to the original expression.
By understanding the logic and steps behind each solution, you can approach similar problems with confidence and improve your problem-solving skills over time.
How to Manage Exam Time Effectively
Time management is crucial during any test. The ability to prioritize tasks, allocate sufficient time to each section, and avoid spending too long on any single question can significantly impact your performance. Planning ahead and staying focused throughout the exam can help you maximize your score.
Key Strategies for Time Management
- Read instructions carefully: Start by quickly reading the instructions for each section. This ensures you understand the requirements and can plan your approach effectively.
- Assess the questions: Quickly scan through the entire test to get an overview of the types of questions. This helps you identify which ones may require more time and which ones can be answered more quickly.
- Prioritize: Tackle questions that you are confident about first. This allows you to secure easy points and gain momentum. Leave more complex or uncertain questions for later.
- Set time limits: Assign a specific amount of time to each question or section, and stick to it. Use a watch or the exam’s timekeeper to track your progress.
How to Stay on Track
- Avoid overthinking: If you get stuck on a question, don’t dwell on it for too long. Move on and return to it later if time allows.
- Leave room for review: Try to finish the test early, giving you time to check your answers for mistakes or areas you may have missed.
- Stay calm: Managing stress is essential for maintaining focus. Take deep breaths if you start feeling rushed, and remind yourself that there’s enough time to complete everything if you manage it well.
By following these strategies, you can effectively manage your time during the exam, ensuring that you answer as many questions as possible and leave no part of the test incomplete.
Reviewing Practice Problems with Solutions
Practicing problems and understanding their solutions is an essential part of mastering any subject. This process helps identify areas of strength and weakness, while also allowing you to become familiar with the types of questions you might encounter. It is important to break down the steps in solving each problem and learn from any mistakes to ensure progress.
Steps for Effective Problem Review
- Start with simpler problems: Begin by solving basic questions to ensure you have a solid foundation. This also helps build confidence before tackling more complex challenges.
- Work through the solution: After attempting a problem, carefully examine the step-by-step solution. Understand why each step is taken and how it leads to the final result.
- Identify mistakes: If an error is made, revisit the concept involved and clarify your understanding. This helps prevent similar mistakes in the future.
- Practice similar problems: After reviewing a problem, solve several more that follow the same steps but vary in numbers or structure. This reinforces the learning process.
Maximizing the Benefits of Practice
- Break problems into parts: If a problem seems overwhelming, break it down into smaller, more manageable steps. Focus on solving one part at a time to avoid confusion.
- Review regularly: Consistent practice is key. Revisiting problems over time helps solidify your understanding and keeps skills sharp.
- Seek clarification when needed: If any concepts remain unclear, ask questions or find additional resources that can provide more detailed explanations.
By actively reviewing and solving practice problems, you can improve your problem-solving skills, deepen your understanding of the material, and gain the confidence needed to perform well in exams.