
Preparing for advanced mathematics assessments can often feel overwhelming, but a focused approach to learning and practice can significantly ease the process. With a structured method, students can build their confidence and improve their problem-solving abilities, ensuring better performance on important tests.
Key to achieving mastery is working through a variety of exercises that cover essential concepts. By engaging with practice materials tailored to specific content areas, learners can sharpen their skills and identify gaps in their understanding. Regular practice, along with a strategic review of the most critical topics, can help students feel more prepared and capable when it comes time to take the exam.
Effective study techniques and a clear focus on the most vital areas of the curriculum will not only help in tackling different types of problems but also enhance overall mathematical fluency. Consistency, combined with the right tools, leads to a more confident and successful exam experience.
Mathematics Exam Preparation Assistance
When approaching the study process for major assessments in mathematics, it’s crucial to have access to resources that help reinforce learning and sharpen problem-solving skills. Practicing with tailored materials allows students to better understand key concepts and strengthens their ability to apply those principles under exam conditions.
Building Confidence with Practice Exercises
Engaging with exercises that cover a range of topics ensures a comprehensive understanding of the material. Repetition and hands-on practice can help reduce anxiety, improve recall, and make complex problems more manageable. As students work through various types of questions, they will be able to identify patterns and solutions more efficiently, preparing them for the actual test environment.
Maximizing Performance through Strategic Preparation
A well-organized approach to studying can make a significant difference. By focusing on critical content areas and using specialized resources to reinforce learning, students can enhance their problem-solving strategies. This proactive method helps maximize performance and ensures that learners feel confident on exam day, equipped with the skills needed to succeed.
Understanding the Importance of Review Materials

Preparation for complex assessments requires a focused approach that targets key concepts and enhances problem-solving abilities. These learning tools provide structured practice that ensures mastery of essential topics, leading to improved performance in tests. They serve as a guide to help students identify areas needing further attention while reinforcing their strengths.
Strategic use of practice exercises allows learners to gain confidence and familiarity with the test format, which can reduce anxiety during the actual exam. By working through targeted problems, students can improve both their speed and accuracy, better preparing them for the challenges ahead. Consistent practice is an essential component of effective learning, helping to solidify knowledge and build a deeper understanding of the material.
Key Topics Covered in Mathematics Assessments
In any comprehensive exam focused on advanced mathematical concepts, it is essential to cover a variety of important topics that test both understanding and application of fundamental principles. These areas are designed to challenge learners and ensure that they have mastered the essential skills required for higher education and real-world problem-solving.
The following topics are typically included in such assessments:
- Linear Equations and Inequalities
- Quadratic Functions and Graphing
- Rational Expressions and Equations
- Exponential and Logarithmic Functions
- Polynomials and Rational Expressions
- Systems of Equations and Matrices
- Probability and Statistics
- Sequences and Series
Each of these areas is essential for building a strong mathematical foundation, and understanding them thoroughly will be key to success in exams. Working through practice problems related to these topics will help solidify understanding and prepare students for a range of question types that may appear during testing.
Effective Strategies for Exam Preparation
Preparing for a challenging mathematics exam requires a strategic approach that maximizes understanding and retention of essential concepts. By implementing focused techniques and using the right tools, students can effectively strengthen their skills and build the confidence needed to succeed. A well-organized study plan can make a significant difference in how efficiently and thoroughly learners grasp the material.
Practice Consistently with Targeted Exercises
Consistent practice is key to improving mathematical abilities. Working through a wide variety of problems helps reinforce understanding and makes complex topics more approachable. By regularly practicing different types of questions, students can identify patterns and develop problem-solving techniques that will benefit them during the exam.
Utilize Time Management Techniques

Effective time management is essential to ensure that all topics are covered and that students do not feel rushed on test day. Breaking study sessions into focused intervals, such as using the Pomodoro technique, allows learners to stay concentrated while avoiding burnout. Setting clear goals for each session helps keep progress on track and ensures comprehensive preparation.
How to Use Review Materials Efficiently
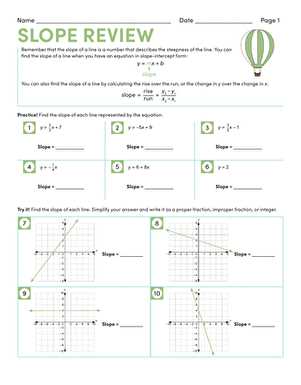
Maximizing the effectiveness of study materials involves more than simply completing exercises. A focused approach can help learners target key concepts and improve their understanding. By using resources in a strategic way, students can enhance their problem-solving abilities and ensure they are well-prepared for their assessments.
Follow these tips for efficient use of study materials:
- Prioritize Difficult Topics: Begin with areas that are challenging or where you feel less confident. This allows you to build a solid understanding before tackling easier concepts.
- Set a Time Limit: Focus on one concept at a time, and spend a set amount of time on each section. Avoid rushing through the material to ensure quality practice.
- Work with Multiple Resources: Don’t rely on just one source. Combining different study tools can help reinforce learning and provide a broader perspective on the topics.
- Review Mistakes: Take time to analyze errors. Understanding why a solution was incorrect is as important as getting the right answer.
- Take Breaks: Studying in intervals with short breaks in between can keep you refreshed and improve focus.
By adopting these strategies, learners can use their study materials more effectively and approach their exams with greater confidence and preparedness.
Mastering Mathematical Concepts with Practice
To truly grasp complex mathematical topics, consistent and focused practice is essential. The more you engage with different types of problems, the better you become at recognizing patterns, applying methods, and solving equations with ease. Working through a variety of exercises helps solidify your understanding and prepares you for real-world applications.
Repetition for Reinforcement
Repetition is one of the most effective strategies for mastering new concepts. By practicing regularly, you strengthen your ability to recall and apply formulas and techniques. Repeated exposure to similar problems allows you to identify subtle differences in approaches and solutions, enhancing both your efficiency and accuracy.
Building Problem-Solving Skills

While memorizing formulas is helpful, developing problem-solving skills is crucial for success. Practice challenges you to think critically and creatively, adapting your approach as needed. Over time, you’ll learn how to break down complex problems into simpler steps and find solutions more quickly and effectively.
Common Mistakes to Avoid in Mathematics
When working through mathematical problems, it’s easy to make simple errors that can affect your overall performance. Recognizing these common pitfalls and taking steps to avoid them can significantly improve your accuracy and problem-solving ability. By addressing these mistakes early, you can build a stronger foundation and approach future challenges with greater confidence.
Here are some common mistakes to be aware of:
- Misinterpreting the Question: Always ensure you fully understand what the problem is asking. Rushing through the wording can lead to missing important details that impact your solution.
- Forgetting to Simplify: After solving a problem, don’t forget to simplify your final expression or solution. Failing to do this can result in incomplete or incorrect answers.
- Incorrectly Applying Formulas: Double-check that you’re using the correct formulas for each problem. Applying the wrong formula can lead to a series of errors in your solution.
- Overlooking Negative Signs: Negative signs can be tricky, and forgetting them can lead to major calculation mistakes. Pay careful attention when adding, subtracting, multiplying, or dividing negative numbers.
- Skipping Steps: Avoid skipping steps in your calculations. Writing out each step helps ensure you don’t miss crucial parts of the process and makes it easier to find errors if your answer doesn’t match expectations.
By being mindful of these common mistakes and working to avoid them, you can improve your problem-solving accuracy and achieve better results in mathematics.
Benefits of Working Through Practice Problems

Engaging with practice problems is one of the most effective ways to solidify understanding and improve problem-solving abilities. By consistently working through a variety of exercises, you develop the skills necessary to approach complex challenges with confidence. This method not only reinforces theoretical concepts but also builds critical thinking and analytical skills that are essential for success in mathematics and beyond.
One of the key advantages of practicing problems is that it helps to identify areas of weakness. When you encounter difficulties, you are given the opportunity to focus on those specific topics and improve. This targeted approach allows for more efficient learning and enhances overall performance.
Additionally, practicing regularly can help increase speed and accuracy. As you become more familiar with the types of problems and methods required to solve them, you can solve similar problems more quickly and with fewer mistakes. This is particularly beneficial when preparing for exams, as it boosts both confidence and efficiency under time constraints.
Moreover, solving problems builds a deeper connection to the material, helping you move from basic recall to a more profound understanding of how different concepts interact. This deeper level of comprehension is crucial when facing more advanced topics or applying mathematical ideas in real-world scenarios.
How to Identify Important Mathematical Topics
Recognizing key topics is essential when preparing for any academic subject. In mathematics, some areas are more frequently tested and have a greater impact on your understanding of the subject. By identifying these crucial areas, you can focus your efforts on mastering the most important concepts and skills needed for success. This targeted approach ensures that you are well-prepared for exams and future challenges.
To determine which topics are most important, consider the following strategies:
- Review Past Exams: Look at previous tests and assignments to identify recurring themes or types of problems. These areas are often emphasized and are likely to appear again.
- Focus on Core Concepts: Core principles like equations, functions, and graphing are fundamental to many areas of mathematics. Mastering these concepts will help you tackle a wide range of problems.
- Consult Your Curriculum: Your course outline or syllabus can provide a roadmap of key topics that you need to study. Prioritize topics marked as essential for your grade level or exams.
- Identify Prerequisites: Certain topics build on previous knowledge. Understanding foundational concepts is necessary before progressing to more advanced material.
- Seek Guidance from Teachers: Instructors often highlight important topics that will be tested. Don’t hesitate to ask for their advice on what to focus on most.
By using these strategies, you can effectively identify the most important areas to study, ensuring a more focused and efficient learning process.
Tips for Tackling Word Problems
Word problems can often feel overwhelming due to their complex nature and the need to translate real-world situations into mathematical equations. However, by breaking down the problem into manageable steps, you can approach these challenges with confidence. The key is to stay organized, understand the problem’s context, and apply the appropriate strategies to find the solution.
Here are some effective tips to help you tackle word problems with ease:
| Tip | Description |
|---|---|
| Read the Problem Carefully | Start by reading the problem slowly and more than once to ensure you understand all the details. Identify what is being asked and the given information. |
| Define Variables | Assign variables to the unknowns in the problem. This makes it easier to set up equations that represent the relationships between different quantities. |
| Look for Keywords | Pay attention to keywords that indicate mathematical operations, such as “total,” “difference,” “product,” or “sum.” These words guide you in forming the correct equations. |
| Set Up an Equation | Based on the information and relationships described in the problem, set up an equation that reflects the situation. Make sure your equation is accurate and aligns with the problem’s details. |
| Solve and Check | Once the equation is set, solve for the unknowns. Afterward, check your solution to see if it makes sense in the context of the original problem. |
By following these steps, you’ll be able to approach word problems systematically and improve your ability to find solutions more efficiently.
Breaking Down Complex Equations
Complex equations can often seem intimidating, especially when multiple variables, operations, and terms are involved. However, by breaking these equations into smaller, more manageable parts, you can approach solving them with confidence. The key is to recognize patterns, simplify terms, and methodically solve for unknowns.
The following strategies can help you break down complex equations and find solutions more efficiently:
Simplify and Combine Like Terms
Start by identifying and combining any like terms on both sides of the equation. This step reduces the complexity of the equation, making it easier to work with. For instance, combine all constants and variables that share the same exponent or degree.
Apply the Order of Operations
When working through complex equations, always follow the correct order of operations: parentheses, exponents, multiplication and division (from left to right), and finally, addition and subtraction (from left to right). This ensures that you are solving the equation step-by-step in the right order.
By approaching complex equations systematically, you can simplify the process and solve for unknowns with greater accuracy. Stay focused on one step at a time, and always double-check your work for any mistakes or missed details.
How to Stay Organized During Your Review
Staying organized during a preparation session is crucial for maintaining focus and effectively managing time. A structured approach helps you prioritize important topics and avoid feeling overwhelmed. The key is to break down the material into smaller sections and track your progress consistently.
One effective strategy is to create a clear plan. Begin by identifying key areas that need attention and allocate specific time slots for each. Use notes, color-coded sections, or diagrams to keep the material visually organized. Keep track of completed sections to see your advancement and identify areas that need further attention.
Additionally, keep your workspace neat and free from distractions. A clean, organized environment can help improve concentration and mental clarity. Regularly take short breaks to avoid burnout and maintain focus throughout the review process.
Using Online Resources to Enhance Learning
In today’s digital age, the internet offers a wealth of resources that can significantly improve your understanding of complex subjects. These tools provide instant access to explanations, practice exercises, and interactive content, making them invaluable for reinforcing concepts and bridging learning gaps.
One of the most beneficial aspects of online resources is their ability to offer a variety of learning styles. Whether you prefer watching video tutorials, reading articles, or engaging in interactive quizzes, there are resources that cater to all preferences. Here are some useful ways to incorporate online resources into your study routine:
- Video Tutorials: Platforms like YouTube and Khan Academy offer step-by-step explanations of various topics. These can be especially helpful for visual learners who benefit from seeing concepts in action.
- Interactive Quizzes: Websites like Quizlet and various educational apps provide quizzes that test your knowledge and reinforce key concepts.
- Forums and Discussion Groups: Engaging in online communities allows you to ask questions, share insights, and learn from others’ experiences, providing a collaborative learning environment.
By using a combination of these resources, you can create a well-rounded approach to studying and deepen your understanding of challenging subjects. The variety of online tools ensures that you can find the support you need, whenever and wherever you need it.
How to Handle Test Anxiety for Algebra 2

Test anxiety is a common challenge that many students face, especially when preparing for a comprehensive exam. This stress can hinder your ability to perform well, even if you have studied thoroughly. The key to overcoming anxiety lies in preparation, mindset, and practical strategies that help you stay calm and focused during the exam.
Preparation is Key
The more prepared you are, the less anxious you’ll feel. Build a structured study schedule that breaks down your material into manageable sections. Here are some effective techniques:
- Consistent Practice: Regularly working through problems helps reinforce concepts and boosts confidence.
- Review Past Work: Analyze previous tests or exercises to identify areas that need improvement.
- Set Realistic Goals: Set small, achievable targets each day to keep you motivated and prevent overwhelming yourself.
Managing Stress During the Exam
Once you sit down for the exam, it’s important to stay calm and focus on the task at hand. Here are some tips for managing stress during the test:
- Deep Breathing: Take a few slow, deep breaths to calm your mind and body before starting.
- Read Carefully: Before jumping into solving problems, take time to carefully read each question to avoid misinterpretation.
- Don’t Rush: Move at a steady pace and avoid getting stuck on difficult questions–move on and come back to them if needed.
By following these strategies, you can reduce anxiety, build confidence, and approach the test with a calm and focused mindset.
Time Management for Exam Preparation
Effective time management is crucial for success when preparing for a challenging test. By organizing your study schedule and using your time wisely, you can cover all necessary material without feeling overwhelmed. The goal is to create a balanced approach that allows you to review key concepts while also allowing time for rest and relaxation.
Creating a Study Schedule
Planning your study sessions in advance ensures you stay on track and make steady progress. Here’s a simple way to structure your time:
| Time of Day | Activity |
|---|---|
| Morning | Review challenging topics or areas of weakness |
| Afternoon | Practice problems to reinforce learning |
| Evening | Light review or flashcards for quick recall |
Prioritizing Key Topics
Focus on the most important subjects that are likely to appear on the test. This includes identifying areas you struggle with and spending extra time on them. Consider the following tips:
- Start with Difficult Topics: Tackle harder subjects when you are freshest in the day.
- Use Short, Focused Sessions: Aim for 30-45 minute study blocks followed by short breaks.
- Review Regularly: Even on days when you don’t have long study sessions, make time for a brief review.
With a well-organized schedule, you can ensure that you’re not only covering all necessary material but also avoiding burnout, leading to better performance on exam day.
Maximizing Resource Use for Exam Success

To excel on any exam, it’s important to use available materials effectively. Proper utilization of study tools can help you stay focused, identify areas of weakness, and track progress. By approaching these resources with a strategic plan, you can ensure you’re prepared and confident on test day.
Structured Approach to Using Study Materials
Having a plan for engaging with study resources is key. Here’s how you can maximize their impact:
| Step | Action |
|---|---|
| 1 | Begin by reviewing the overall structure of the material to understand the key concepts covered. |
| 2 | Identify areas where you feel less confident and focus on those first. |
| 3 | Break down complex sections into smaller, manageable chunks and tackle them one at a time. |
| 4 | Use practice questions to reinforce learning and measure understanding. |
| 5 | Review any mistakes and focus on the concepts you struggled with. |
Staying Consistent and Focused
Consistency is vital. Set aside time each day for focused study sessions, and try to avoid cramming the night before the exam. Regular practice, combined with efficient use of resources, helps reinforce knowledge over time. Additionally, make sure to take regular breaks to keep your mind fresh and focused throughout your sessions.
By following these steps and maintaining a disciplined approach, you can use study tools to their fullest potential, giving you the best chance for success on exam day.
Review Resources for Students in Advanced Mathematics
For students preparing for assessments in advanced mathematics, having the right resources is essential for reinforcing key concepts and building confidence. Utilizing structured materials effectively can help identify areas of improvement and enhance problem-solving skills. There are a variety of tools available that cater to different learning styles, making it easier to master challenging topics and excel on exams.
Types of Resources to Explore
Several types of resources can help students gain a better understanding of mathematical concepts:
- Practice Worksheets: These allow students to solve problems related to the material covered in class, offering a hands-on approach to reinforcing knowledge.
- Online Tutorials: Video lessons and step-by-step guides provide in-depth explanations of complex topics, offering visual learners an opportunity to follow along and practice.
- Interactive Websites: Websites with interactive exercises can give instant feedback, helping students learn from their mistakes and improve their skills.
- Flashcards: Digital or physical flashcards can help with memorization of formulas and key definitions, making it easier to recall information during assessments.
Effective Strategies for Using Resources
To make the most of these resources, students should approach them strategically:
- Prioritize Areas of Difficulty: Focus on topics that are most challenging and allocate additional study time for them. This helps ensure that you are fully prepared for all aspects of the exam.
- Consistency is Key: Set a study schedule and stick to it, working on different materials each day to reinforce knowledge in a structured way.
- Seek Help When Needed: Don’t hesitate to ask for clarification on difficult topics. Whether it’s from a teacher, tutor, or peer, understanding challenging concepts will help you build a solid foundation.
By using a variety of study materials and adopting effective strategies, students can improve their understanding and feel well-prepared for any exam in advanced mathematics.