
This part of the learning resource offers valuable support for solving complex problems and understanding key mathematical principles. By focusing on various topics, it guides students through the process of mastering challenging tasks and reinforces critical concepts. Whether for review or practice, the resource is designed to make the learning experience smoother and more efficient.
The material is structured to provide clear explanations and detailed solutions, breaking down difficult problems into manageable steps. This approach allows learners to grasp each concept at their own pace, ensuring they build a solid foundation for future studies. With interactive tools and easy-to-follow guidance, it encourages independent problem-solving while fostering confidence in tackling advanced topics.
For those seeking to improve their skills or prepare for assessments, this section serves as an essential tool. The comprehensive answers and tips provided help users not only understand the reasoning behind each solution but also develop strategies for applying these methods in various contexts.
Comprehensive Guide to Solving Advanced Problems
This segment focuses on providing learners with detailed methods to approach and resolve challenging exercises. It serves as a roadmap for breaking down intricate concepts into understandable parts, helping users strengthen their comprehension and application skills. By engaging with these materials, students can build confidence in tackling progressively complex topics.
The explanations included here are designed to illuminate the reasoning behind each solution. Step-by-step instructions encourage critical thinking and ensure learners can apply the techniques independently in similar scenarios. This structured approach fosters a deeper understanding of essential principles and their real-world applications.
Additionally, this part offers insights into common errors and how to avoid them, making it a valuable tool for refining problem-solving strategies. By practicing with these resources, users can enhance their proficiency and prepare effectively for future challenges.
Overview of Algebra Nation Section 9
This part of the learning resource is dedicated to providing in-depth support for mastering key mathematical concepts. It offers detailed guidance for students looking to enhance their problem-solving abilities, with a focus on progressively difficult exercises. The section is designed to break down complex topics into manageable steps, making it easier for learners to grasp difficult ideas and build strong foundations for future study.
Structure of the Material
The content is organized in a way that gradually increases in complexity, allowing users to start with simpler tasks before moving on to more challenging problems. Each exercise is accompanied by a detailed explanation, ensuring learners understand the process behind every solution. This structure helps reinforce the learning experience and encourages critical thinking at every step.
Benefits for Learners
This section helps students develop a deeper understanding of fundamental concepts, making them more confident in their ability to tackle advanced topics. With a focus on practice and application, it serves as an essential tool for both reviewing and mastering complex subjects. By working through the material, users gain not only the solutions but also the reasoning and strategies needed to excel in similar problems.
How to Use the Answer Key
This resource is designed to help students navigate through complex problems by providing clear, step-by-step solutions. To make the most of this tool, it is essential to approach it strategically–using it not only for finding the correct results but also for understanding the reasoning behind each solution. This approach helps in developing a deeper understanding of the material and applying the techniques independently in future tasks.
Step-by-Step Guidance
When using this material, it is important to start with an attempt to solve the problem on your own. Afterward, compare your method with the provided solution. Pay close attention to the steps involved and identify the logic behind each one. This method helps you learn the correct approach while also improving your critical thinking skills. By focusing on the reasoning rather than just the final result, you can build a stronger grasp of the subject.
Common Mistakes to Avoid
While utilizing this tool, be mindful of common pitfalls that may arise. Often, students may rush through the solutions without thoroughly understanding each step. This can lead to confusion or errors in applying the methods to new problems. Instead, take time to review the logic behind every solution and ensure you are not simply memorizing steps, but understanding the principles that govern them. This practice will improve both accuracy and long-term retention.
Step-by-Step Solutions for Section 9
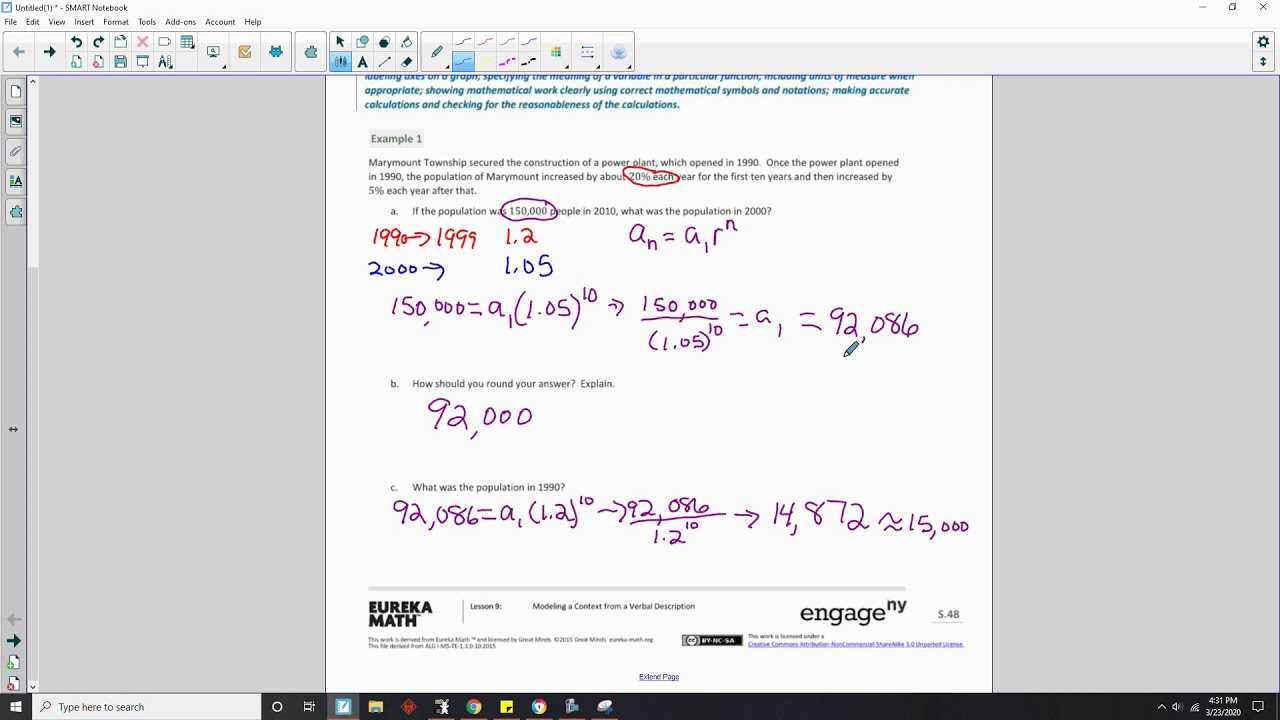
This part provides a detailed breakdown of the exercises, offering a structured approach to solving each problem. The solutions are presented in a clear, logical sequence, helping learners follow along and understand the underlying principles. By breaking down the problems into smaller steps, students can easily grasp each concept and improve their problem-solving abilities.
Follow these steps to work through each exercise:
- Read the problem carefully to understand the given information and what needs to be solved.
- Identify key concepts or formulas that might be applicable to the task.
- Work through the problem step by step, ensuring each part is understood before moving to the next.
- Check your solution against the provided steps, ensuring your logic matches the detailed explanation.
- Review any mistakes and try to understand why they occurred to avoid repeating them in the future.
By following these steps, learners can gain a deeper understanding of how to approach and solve similar problems independently.
Common Mistakes to Avoid
While solving mathematical problems, it’s easy to make errors that can lead to incorrect results or misunderstandings of key concepts. Identifying and avoiding these common mistakes is essential for improving your problem-solving skills and achieving more accurate solutions. By being aware of these pitfalls, you can ensure a smoother learning experience and strengthen your understanding of the material.
Common Errors in Problem Solving
- Rushing through the steps without fully understanding each one.
- Misinterpreting the question or missing key details in the problem.
- Using incorrect formulas or applying them inappropriately.
- Skipping over intermediate steps, which can lead to calculation mistakes.
- Failing to double-check work, which may result in overlooked errors.
Strategies for Avoiding Mistakes
- Take time to read the problem carefully and highlight important information.
- Always check the steps after completing them to ensure accuracy.
- Understand the rationale behind each formula or technique before applying it.
- Practice problems regularly to improve familiarity with different types of questions.
- Seek feedback or review solutions to learn from past mistakes.
By staying mindful of these common mistakes and actively working to avoid them, you can improve both your accuracy and efficiency in solving similar tasks in the future.
Key Concepts Covered in Section 9
This part of the material focuses on fundamental ideas and methods that form the backbone of solving complex mathematical tasks. It highlights the essential principles that learners need to understand in order to approach problems with confidence and precision. By mastering these key concepts, students will be better equipped to handle more advanced topics in the future.
Core Mathematical Principles
Throughout this section, several key ideas are emphasized, such as:
- Understanding the relationship between variables and constants in equations.
- Mastering different techniques for simplifying complex expressions.
- Applying advanced problem-solving strategies to real-world scenarios.
- Identifying patterns and utilizing them for efficient solutions.
Building a Strong Foundation
By focusing on these critical concepts, this section aims to build a strong foundation that will support the learning of more challenging material. Grasping these fundamental principles is essential not only for academic success but also for developing problem-solving skills applicable in various contexts.
Improving Your Mathematical Skills with Section 9
This part of the resource is designed to help students enhance their understanding and proficiency in solving mathematical problems. By providing structured guidance, it focuses on building critical thinking and problem-solving abilities. Engaging with these materials will not only improve your skills in solving current exercises but also prepare you for more advanced challenges ahead.
Strategies for Effective Practice

To get the most out of this material, consider applying the following strategies:
- Start by working through each problem at your own pace, ensuring you understand the process before moving on.
- Practice regularly to strengthen your familiarity with different types of problems.
- Review solutions step by step to grasp the reasoning behind each technique and method.
- Use the explanations to identify areas where you might need more practice and focus on those specific skills.
Building Confidence for Advanced Topics
With consistent practice and a focus on the fundamental principles, this section will help you build the confidence needed to tackle more complex problems. The goal is not only to find the right answers but to develop a deeper understanding of the underlying concepts. This approach will enable you to apply what you’ve learned to new and unfamiliar tasks, ensuring long-term success in future studies.
Understanding Problem-Solving Techniques
Mastering problem-solving methods is essential for effectively tackling mathematical challenges. This section introduces various strategies that help break down complex tasks into manageable steps. By understanding these techniques, students can approach problems more confidently and apply logical reasoning to find solutions.
Some of the most important techniques involve identifying patterns, simplifying problems, and using different approaches to test possible solutions. Each method is designed to build critical thinking skills and help students think more strategically when solving problems.
With consistent practice, these techniques will not only improve accuracy but also increase the efficiency of solving various types of problems, making even the most difficult tasks more approachable.
Why This Resource is Helpful
This platform is a valuable tool for learners aiming to strengthen their problem-solving skills and gain a deeper understanding of mathematical concepts. It provides structured guidance, clear examples, and a range of exercises designed to help students master essential techniques. By offering a step-by-step approach, it supports learners in navigating through complex topics and improves their ability to apply what they’ve learned in practical situations.
Here are some reasons why this resource is so effective:
- Clear Explanations: Each problem is broken down into manageable steps, making it easier for students to follow and understand.
- Comprehensive Coverage: The platform covers a wide range of topics, from basic concepts to more advanced methods, allowing students to progress at their own pace.
- Interactive Learning: It encourages active engagement by providing opportunities to practice and review material, helping students reinforce their knowledge.
- Instant Feedback: Learners can check their solutions and immediately identify any mistakes, improving their learning experience.
With its focused approach, this resource helps learners gain confidence in their abilities, ensuring they can tackle a variety of mathematical problems with ease.
Using the Answer Resource for Self-Study
Self-study is a powerful way to enhance your understanding of complex topics. By utilizing a solution guide, learners can independently verify their answers, identify mistakes, and understand the process behind each step. This approach promotes critical thinking and helps reinforce the concepts learned during practice.
Here’s how to make the most of this resource for effective self-study:
- Work Through Problems First: Before referencing the solution guide, attempt each problem on your own to strengthen your problem-solving skills.
- Check Your Work: After completing an exercise, compare your solution with the one provided in the guide to ensure accuracy.
- Understand the Process: Don’t just focus on the final answer. Study the steps and reasoning used to solve the problem, as this will help deepen your understanding.
- Identify Mistakes: If your solution differs from the guide, take the time to analyze where you went wrong and learn from those mistakes.
- Repetition: Rework similar problems and use the solution guide to ensure you are applying the correct methods consistently.
By following these steps, self-study becomes an effective tool for mastering topics and improving your overall problem-solving abilities.
How Section 9 Builds Mathematical Confidence

Mastering challenging concepts can significantly boost one’s confidence in problem-solving. By engaging with structured exercises, learners can develop a deeper understanding and a stronger sense of achievement. The practice of tackling problems independently, while having access to resources for verification, helps students become more assured in their abilities.
Building a Strong Foundation
Section 9 is designed to provide learners with a solid foundation in key topics. By working through well-structured examples and problems, students are guided step by step, allowing them to gradually build the necessary skills and insights. This incremental approach ensures that learners are not overwhelmed, while still being challenged enough to make progress.
Reinforcing Confidence Through Practice
Continuous practice is essential for strengthening mathematical confidence. As students solve increasingly complex problems, they gain confidence in their ability to apply learned techniques. The ability to self-check and understand the reasoning behind each solution encourages a sense of mastery and reduces self-doubt.
Ultimately, by engaging with the materials in Section 9, students develop a stronger sense of confidence in their problem-solving skills, which will carry over to future challenges in mathematics and beyond.
Top Strategies for Math Success
Achieving success in mathematics requires a combination of consistent practice, effective techniques, and the right mindset. By implementing a few key strategies, learners can improve their problem-solving abilities and gain a deeper understanding of the subject. The following strategies are designed to help students excel and build confidence in their mathematical skills.
Master the Fundamentals
Building a strong foundation is crucial for tackling more advanced problems. Start by thoroughly understanding basic concepts, as these are the building blocks for more complex topics. Whether it’s understanding basic operations or fundamental principles, mastering these early lessons ensures greater success later on.
Practice Regularly and Review Mistakes
Repetition is key to reinforcing learning. Regularly working through problems allows students to become familiar with different problem types and solutions. Additionally, reviewing mistakes is a powerful tool for improvement. Analyzing errors helps identify areas for further study and ensures that incorrect methods are corrected for future problems.
Additional Tips:
- Stay Organized: Keep track of your progress and review notes regularly to stay on top of the material.
- Ask for Help: Don’t hesitate to reach out for guidance when needed–collaboration can often lead to a deeper understanding.
- Stay Positive: Cultivating a positive mindset will help you stay motivated and overcome difficult challenges.
By using these strategies, learners can approach mathematical problems with confidence, steadily improving their skills and achieving greater success in the subject.
Mastering Mathematics with Section 9 Solutions
Achieving mastery in mathematics requires a strategic approach to problem-solving and continuous practice. Utilizing a resource that provides detailed solutions can significantly enhance your understanding of complex concepts. By working through problems and comparing your methods to those in the solutions guide, you can identify areas for improvement and solidify your grasp on the material.
Section 9 solutions offer a comprehensive breakdown of essential techniques and strategies. These solutions not only provide the correct outcomes but also show the step-by-step processes behind each problem, helping learners understand how to approach similar challenges in the future. This method of guided practice is particularly effective for building confidence and reinforcing core principles.
By regularly referring to solutions, students can track their progress, correct mistakes, and gradually master new mathematical concepts with increasing ease and accuracy. Through consistent use of these resources, learners can achieve greater proficiency and confidence in their problem-solving abilities.
Exam Preparation Tips for Section 9
Preparing for exams can be a challenging yet rewarding process. To succeed in any assessment, it is important to focus on the most effective study strategies. A solid understanding of key concepts, combined with practical problem-solving exercises, can significantly improve your performance. Here are some tips to help you prepare efficiently and perform confidently on your exam.
1. Review Key Concepts
Start by reviewing the foundational concepts that will be tested. Understanding the theory behind each problem type allows you to approach questions methodically. Focus on areas that are historically challenging for you or where you have encountered difficulties in previous exercises.
2. Practice with Examples
Working through practice problems is one of the best ways to prepare for any test. Use practice questions from your study resources or solve problems similar to those you expect on the exam. This will help you familiarize yourself with the types of problems and improve your speed and accuracy under time constraints.
3. Identify Common Mistakes
While practicing, make a note of the mistakes you commonly make. Understanding where you tend to go wrong will allow you to focus on correcting those areas. It’s also helpful to learn the correct methods and strategies to avoid these errors in the future.
4. Take Timed Practice Tests
Simulate exam conditions by taking timed practice tests. This will not only help you become more comfortable with the format but also allow you to manage your time effectively during the actual exam. Try to solve the problems within the allotted time to ensure that you can complete the exam without feeling rushed.
5. Stay Calm and Confident
Lastly, maintain a calm and focused mindset before and during the exam. Confidence comes from preparation, so trust in the work you’ve put in. Don’t rush through problems–take your time to think critically and apply what you’ve learned.
By following these tips, you can improve your performance and increase your chances of success on exam day. Proper preparation leads to confidence and, ultimately, better results.
Additional Resources for Algebra Learners
For those looking to enhance their understanding and skills, there are a variety of tools and materials available. These resources can complement your learning by offering extra practice, detailed explanations, and interactive lessons. Whether you’re seeking help with basic concepts or more advanced techniques, using diverse study materials can help solidify your knowledge and boost your confidence.
Online Platforms
Several websites offer free or paid tutorials, practice problems, and interactive exercises. These platforms allow learners to study at their own pace and revisit topics as needed. Many platforms also provide video tutorials that explain complex concepts in a simple and visual manner.
Books and Guides
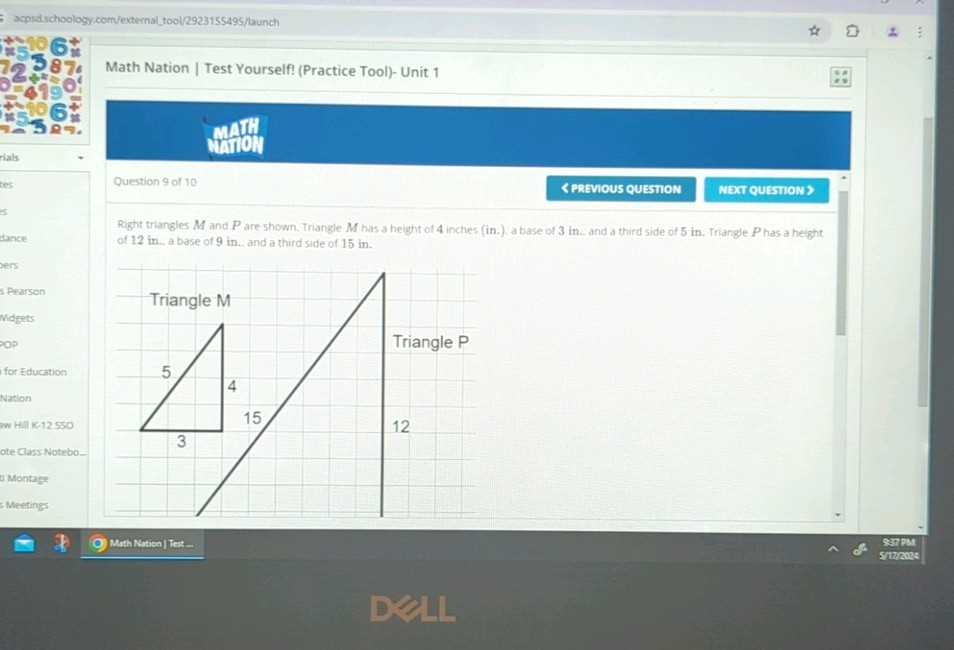
In addition to online resources, many textbooks and study guides are available to reinforce key concepts. These often include worked-out examples, practice problems, and tips to help students excel. Some guides focus on specific areas, while others cover a broader range of topics.
| Resource Type | Platform/Book Name | Description |
|---|---|---|
| Online Platform | Khan Academy | Free educational platform offering comprehensive lessons and exercises across various topics. |
| Book | Precalculus: Mathematics for Calculus | Textbook with in-depth explanations, exercises, and practice questions. |
| Interactive Learning | Wolfram Alpha | Computational knowledge engine for solving math problems step-by-step. |
| Video Tutorials | PatrickJMT | Popular YouTube channel providing math tutorials and solutions to common problems. |
By utilizing these additional materials, learners can gain a more comprehensive understanding of the subject, explore different methods of solving problems, and reinforce what they’ve already learned. These resources are valuable tools for anyone committed to improving their skills and achieving success in their studies.
How Section 9 Prepares You for Future Topics
The material covered in this part of the course plays a crucial role in laying a strong foundation for more advanced topics in mathematics. By mastering the core concepts, learners develop problem-solving skills that are essential for tackling future challenges. As you progress, the concepts introduced here will be applied in increasingly complex scenarios, making it essential to fully understand the fundamentals.
Building a Strong Mathematical Foundation
In this section, the focus is on understanding core mathematical principles that are widely used in higher-level subjects. Mastery of these concepts helps in making connections between different areas of study. As students continue their education, these foundational ideas serve as building blocks for more specialized subjects, such as calculus, statistics, and linear algebra.
Transitioning to Advanced Problems
By practicing and solving the types of problems presented, learners develop techniques and strategies that they can carry forward into future topics. The experience gained from solving increasingly challenging exercises in this section prepares students to confidently approach more complex mathematical problems. The problem-solving approach and reasoning skills sharpened here are directly applicable to tackling future coursework.
Interactive Features of Algebra Nation
The platform offers a variety of interactive tools designed to engage users and enhance their understanding of mathematical concepts. These features provide a dynamic learning experience, allowing learners to practice and apply their knowledge in real-time. By using interactive elements, students can receive immediate feedback and track their progress, making the learning process more effective and enjoyable.
Interactive Practice Problems

One of the most beneficial tools available is the interactive set of practice problems. These exercises are tailored to challenge learners and help reinforce concepts covered in lessons. As students solve these problems, they receive instant feedback, allowing them to identify areas where they may need further improvement.
| Feature | Benefit |
|---|---|
| Instant Feedback | Helps identify errors and correct them immediately, reinforcing learning. |
| Progress Tracking | Allows learners to monitor their growth and focus on areas needing improvement. |
| Customizable Difficulty | Adjusts problem difficulty based on the learner’s performance, ensuring appropriate challenges. |
Engaging Video Lessons

Another key feature is the interactive video lessons. These videos not only explain complex ideas but also offer on-screen prompts and questions that encourage active participation. Learners can pause, replay, and interact with these videos to deepen their understanding and ensure mastery of each concept.
Understanding the Structure of Section 9
The layout of this part of the curriculum is designed to guide learners through various concepts in a logical and organized manner. Each segment is carefully structured to ensure that foundational ideas are introduced first, with more advanced topics building upon them. This format allows students to progress step-by-step, mastering key ideas before moving on to the next challenge.
Key Components of the Structure
- Introduction to Concepts: Each section begins with an overview that explains the main ideas and objectives to be covered.
- Practice Problems: After the explanation, learners are provided with exercises to apply the knowledge they’ve just gained, reinforcing their understanding.
- Real-Life Applications: Some sections include practical examples that show how the concepts can be applied in real-world situations, helping to contextualize the material.
- Review and Assessment: A final review section ensures that students can reflect on what they’ve learned and test their mastery of the subject matter.
How Each Part Builds on the Next
The structure is not just linear but also cumulative, with each part of the material reinforcing earlier lessons. By reviewing and applying previous concepts before moving on, students solidify their understanding and prepare themselves for the next topic. This approach ensures that the learning experience is progressive and coherent, reducing confusion and helping students retain more information.