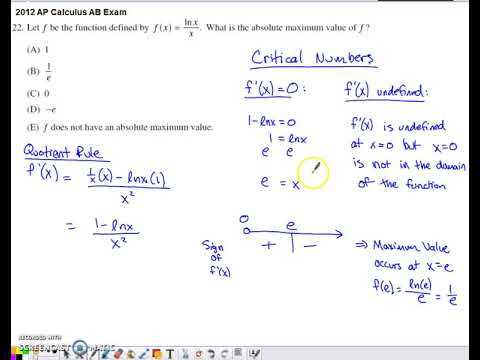
The assessment for advanced mathematics is a critical component for students aiming to demonstrate their understanding and skills in the field. It requires both preparation and strategic thinking, particularly when it comes to answering the section that tests one’s ability to quickly solve problems and analyze complex scenarios. Achieving a high score involves mastering specific techniques and being able to apply them effectively under time constraints.
Success in this part of the evaluation relies on recognizing patterns in questions, applying fundamental principles, and making accurate calculations. With the right approach, students can boost their confidence and improve their performance significantly. Careful study and review of core concepts play an important role in securing a top score.
In this section, we will discuss key strategies for tackling the questions efficiently, providing helpful tips to enhance your problem-solving abilities. Understanding what to expect and how to approach each challenge is essential for achieving success in the timed portion of the test.
Overview of the AP Advanced Mathematics Test
This test is designed to assess a student’s understanding of key mathematical principles and their ability to apply these concepts in problem-solving. It challenges individuals to demonstrate proficiency in various topics, including functions, rates of change, and integrals, through a structured series of questions. The assessment is divided into different segments, each focusing on distinct areas of mathematical knowledge.
In the first section, students encounter questions that evaluate their grasp of foundational theories, requiring both theoretical and practical knowledge. These questions are meant to test their ability to interpret and manipulate mathematical ideas. In the second section, the emphasis shifts to applying these principles in more complex scenarios, requiring critical thinking and precision.
Success in this evaluation hinges on strong preparation, clear understanding of the subject matter, and the ability to quickly and accurately work through problems. Proper study strategies and familiarity with the test format are key components in achieving a high score.
Understanding the Multiple Choice Format
The assessment consists of a series of questions that require students to select the correct answer from a list of options. This format is designed to test both knowledge and the ability to make quick decisions based on mathematical principles. Each question presents a scenario or problem, followed by several possible solutions. The challenge lies in recognizing the right approach and applying it effectively under time constraints.
Structure of the Section
The section is organized into different groups of questions that cover various topics. Each question is designed to test specific skills, such as problem analysis, computation, and concept application. Students are expected to identify the correct solution and demonstrate their understanding of the material.
Time Management and Strategy
With limited time to complete the section, students must manage their time wisely. Prioritizing questions based on familiarity and difficulty can help improve performance. It is important to read each question carefully, eliminate obviously incorrect options, and make an educated guess when unsure.
| Topic | Number of Questions | Key Focus Areas |
|---|---|---|
| Functions and Graphs | 12 | Understanding function behavior, graph interpretation |
| Rates of Change | 8 | Solving problems involving derivatives |
| Integrals | 10 | Finding areas and solving integral problems |
Key Topics Covered in the Exam
This assessment focuses on several core mathematical principles that require both understanding and application. Students are expected to demonstrate their proficiency in a range of areas, from basic functions to more complex concepts like rates of change and areas under curves. These topics are crucial for solving problems effectively and efficiently, and mastering them is key to performing well.
The following areas are emphasized throughout the test:
- Functions and Graphs – Understanding different types of functions and how to interpret their graphs is essential for solving related problems.
- Rates of Change – This includes working with derivatives to solve problems involving motion, growth, and decay.
- Definite Integrals – Students are required to calculate areas and solve problems involving integration techniques.
- Applications of Derivatives – Applying the concept of derivatives to real-world scenarios such as optimization and motion analysis.
- Limits – Comprehending and solving problems related to limits is a critical foundation for understanding continuous change.
Familiarity with these topics is fundamental for navigating the assessment successfully, as they form the backbone of many questions and problem-solving scenarios. A strong grasp of each area ensures that students can quickly apply the right method and choose the correct approach to each challenge.
How to Prepare for AP Advanced Mathematics
Preparation for this assessment requires a strategic approach that involves both mastering the material and practicing under test conditions. A well-rounded study plan focuses on reinforcing key concepts, improving problem-solving skills, and familiarizing yourself with the test format. Diligent practice, combined with time management, is essential for maximizing performance.
Step-by-Step Preparation Tips
To effectively prepare for the assessment, consider the following steps:
- Review Core Concepts – Start by revisiting the fundamental principles of mathematics, including functions, derivatives, and integrals.
- Practice Problem Sets – Regularly solve practice problems to build confidence and improve your ability to apply concepts in different scenarios.
- Focus on Weak Areas – Identify areas where you struggle the most and dedicate extra time to mastering these topics.
- Take Timed Practice Tests – Simulate exam conditions by taking practice tests under timed conditions to improve speed and accuracy.
- Review Test Strategies – Familiarize yourself with common question types and develop strategies for answering them efficiently.
Additional Study Resources
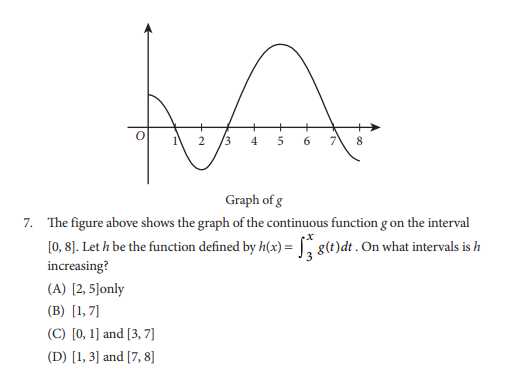
In addition to self-study, using external resources can enhance your preparation:
- Textbooks and Review Guides – Use textbooks to reinforce foundational concepts and review guides for targeted practice.
- Online Tutorials and Videos – Access online platforms that offer instructional videos and explanations for difficult topics.
- Study Groups – Join study groups to collaborate with peers and exchange tips, solutions, and insights.
By following these strategies and using the right resources, you will be well-prepared for the challenges ahead and increase your chances of success.
Test-Taking Strategies for Success
Effective strategies during the assessment can make a significant difference in your performance. Knowing how to approach each question and managing your time wisely are crucial elements that contribute to a high score. With the right mindset and preparation, you can navigate the test with confidence and efficiency.
Stay Calm and Focused – Stress can hinder your ability to think clearly, so it’s important to stay calm throughout the test. Take deep breaths and focus on each question one at a time. If you find yourself stuck, move on to another question and come back later with a fresh perspective.
Read Questions Carefully – Pay close attention to every detail in each question. Often, the wording can contain subtle hints about the right approach. Make sure you understand what’s being asked before jumping to an answer.
Eliminate Incorrect Answers – If you’re unsure about a particular question, eliminate the options that are clearly wrong. This will increase your chances of selecting the correct answer even if you have to guess.
Work Efficiently – Time management is essential. Don’t linger too long on any one question. If you’re unsure, make an educated guess and move on. Save time at the end to review any questions you might have missed.
Use Available Resources – If allowed, use calculators or notes to your advantage. Be familiar with the tools you can use and know when to apply them effectively during problem-solving.
Check Your Work – If time permits, review your answers to ensure you didn’t make any simple mistakes. Double-check your calculations and reasoning to avoid avoidable errors.
By implementing these strategies, you’ll be able to approach the test methodically and confidently, maximizing your performance and achieving your desired outcome.
Common Mistakes to Avoid
Even the most prepared students can make avoidable mistakes during the test. Understanding and recognizing these common pitfalls is key to improving your score. By being aware of these errors and knowing how to prevent them, you can enhance your overall performance and avoid costly missteps.
| Mistake | Why it Happens | How to Avoid It |
|---|---|---|
| Rushing through questions | In a time-limited situation, students often rush to finish quickly. | Take your time, read each question thoroughly, and manage your time wisely. |
| Misreading the question | Confusing key terms or overlooking important details can lead to errors. | Pay close attention to every word and ensure you understand the problem before answering. |
| Skipping difficult questions | Students often skip tough problems, thinking they can return to them later. | Try to answer each question to the best of your ability, even if it means making an educated guess. |
| Overcomplicating solutions | Attempting to apply complex methods when simpler ones are available can lead to mistakes. | Use the most straightforward method first and double-check your work before proceeding. |
| Not checking work | After completing a question, students often skip the review process due to time constraints. | Reserve time at the end of the test to review and double-check your answers for any mistakes. |
Avoiding these common mistakes can help you approach the test with greater confidence and precision, ultimately improving your chances of success.
Time Management During the Exam
Effectively managing your time during the test is crucial for ensuring you have enough opportunity to answer all questions thoroughly. Without proper time allocation, you risk running out of time on harder problems, or spending too much time on simpler ones. Developing a strategy for how to approach the test can help maintain a steady pace and increase your chances of success.
Prioritize and Pace Yourself
At the start of the test, quickly skim through all the questions to get a sense of their difficulty. Prioritize questions that are easier and faster to solve, leaving more time for complex ones. Allocate a certain amount of time to each section and stick to it, ensuring you don’t spend too long on any one question.
Monitor Your Progress
Regularly check the clock to ensure you’re staying on track. If you find yourself spending too much time on a single problem, make a note to return to it later. Maintaining a consistent pace will prevent last-minute rushes and help you stay focused throughout the assessment.
Remember, managing your time effectively is about working smarter, not harder. By practicing these strategies, you can maintain control over your pace and complete the test with confidence.
Using Practice Tests Effectively

Practice tests are a valuable tool for preparing for any assessment. When used properly, they help familiarize you with the format of the questions, improve your time management skills, and highlight areas where you need additional review. The key is not just taking these tests, but using them strategically to maximize your learning.
Here’s how to use practice tests to their full potential:
- Start with Untimed Practice – Begin by completing practice tests without time constraints to get a sense of the material and question structure.
- Focus on Understanding Mistakes – After each practice test, thoroughly review your errors. Understand why the correct answer is right and why the wrong options don’t work.
- Simulate Test Conditions – Once you’re comfortable with the material, take timed practice tests to mimic the real test environment. This will help you build speed and focus.
- Track Your Progress – Keep track of your performance on each practice test. Identify patterns in the types of questions you struggle with and review those areas.
- Review Strategically – Use practice tests to target specific weak areas, and avoid spending too much time on topics you’ve already mastered.
By following these strategies, practice tests can become a powerful part of your study routine. They provide both valuable insights into your progress and opportunities to refine your approach before the actual test.
How to Handle Trick Questions
Trick questions are designed to test your attention to detail and ability to think critically. They often contain misleading wording or require careful interpretation. The key to handling these questions is staying alert and taking your time to fully understand what is being asked before selecting an answer.
Read Carefully – Pay close attention to every word in the question. Look for subtle clues or phrases that might indicate the question is trying to mislead you. Words like “always,” “never,” or “except” can often be key to understanding the correct answer.
Look for Extremes – Trick questions sometimes use extreme statements to confuse you. If an answer choice seems too broad or absolute, take a moment to question it. For example, if a statement says something is true “in all cases,” it’s worth checking whether exceptions exist.
Check for Assumptions – Be cautious of questions that assume you know specific information or that imply something without stating it clearly. Always make sure you’re not falling into the trap of assuming what the question means, rather than what it actually asks.
Double-Check for Negatives – Many trick questions involve negative wording. Make sure to carefully consider any negations in the question and determine how they affect your answer choice. Read through the question twice if needed.
Take Your Time – While managing your time is important, don’t rush through the tricky questions. Take a few extra seconds to reflect on the wording and eliminate answers that don’t make sense. Staying calm and methodical will help you avoid being caught off guard by these questions.
By applying these strategies, you can approach trick questions with confidence and avoid falling into common traps, ensuring that your responses are as accurate as possible.
Reviewing Key Calculus Concepts
A solid understanding of fundamental concepts is essential for tackling complex problems in any test. By focusing on the core principles, you can build a strong foundation and improve your problem-solving skills. Reviewing the most important topics will help you approach questions with greater confidence and efficiency.
Understanding Limits and Continuity
One of the most important concepts is understanding limits and how they define the behavior of functions. Limits help determine the value a function approaches as the input gets closer to a certain point. A strong grasp of this topic is critical for solving problems related to derivatives and integrals.
Mastering Derivatives and Integrals
Derivatives represent the rate of change and are fundamental in understanding motion, optimization, and various real-world phenomena. Similarly, integrals deal with accumulation and area, serving as the inverse operation to derivatives. Reviewing the rules for differentiating and integrating functions will help you solve many types of problems efficiently.
By revisiting these core topics, you’ll be better equipped to handle the more challenging aspects of the subject. A thorough understanding of these concepts ensures you can tackle a wide range of problems with confidence and accuracy.
Tips for Memorizing Formulas
Memorizing formulas can be one of the most challenging aspects of preparing for a test. However, with the right techniques, you can enhance retention and recall when needed. The key is to break down complex equations into simpler components and use strategies that make memorization more efficient and effective.
Use Mnemonics and Acronyms
One of the most effective ways to remember formulas is to create mnemonics or acronyms. These memory aids can help you recall complex relationships between variables by associating them with familiar words or phrases. For example, creating a simple phrase or image that connects to the structure of a formula can make it much easier to remember.
Practice with Flashcards
Flashcards are a powerful tool for reinforcing memory. Write the formula on one side and its meaning or application on the other. Regularly reviewing these flashcards will help reinforce your understanding and solidify the formulas in your long-term memory. The more frequently you test yourself, the more likely you are to remember the formulas under pressure.
Additionally, practice applying the formulas in different contexts. The more you use them in problems, the more familiar they will become. Active engagement with the material will help strengthen your memory and ensure you can recall formulas quickly during the test.
Improving Problem-Solving Skills
Effective problem-solving is a crucial skill for tackling complex questions in any test or real-world scenario. The ability to break down problems, identify patterns, and apply the right strategies can significantly enhance your performance. By practicing structured approaches and developing a logical mindset, you can improve both your speed and accuracy when solving challenging tasks.
Break Problems into Smaller Steps
When faced with a complex problem, it’s easy to feel overwhelmed. One of the best ways to approach it is by breaking it down into smaller, more manageable steps. This method not only simplifies the problem but also allows you to focus on one part at a time, reducing the likelihood of mistakes.
- Identify what is given and what is unknown.
- Determine which principles or methods are most appropriate to solve the problem.
- Work through each step methodically, checking your progress along the way.
Develop a Strategy for Each Problem

Every type of problem may require a different approach. Familiarize yourself with a variety of problem-solving strategies so you can quickly recognize which to apply. Some common strategies include:
- Using algebraic manipulation to simplify expressions.
- Drawing diagrams to visualize the problem.
- Checking for patterns that may help you predict outcomes.
Consistently applying these strategies will help you approach new problems with confidence and clarity. The more problems you solve, the more intuitive these approaches will become, improving both your efficiency and accuracy.
Understanding Graphing Techniques
Mastering graphing techniques is a vital skill for interpreting and solving problems in mathematics. Graphs provide a visual representation of data, relationships, and functions, making it easier to understand complex concepts and identify patterns. Developing the ability to accurately plot and analyze graphs will not only help you solve problems but also strengthen your overall problem-solving abilities.
Plotting Key Points and Features
When working with graphs, it’s crucial to understand how to plot important points and features. Start by identifying key values, such as intercepts, maximum and minimum points, and asymptotes. These features provide important information about the behavior of the function. Once identified, plot them accurately on the graph to create a clear and informative visual representation.
Understanding the Behavior of Functions
Another key aspect of graphing is interpreting the behavior of functions across different intervals. By analyzing the slope, concavity, and other characteristics of a graph, you can determine how the function behaves as the input changes. This understanding allows you to make predictions and gain insights into the problem at hand.
By practicing these techniques and becoming comfortable with graphing, you’ll be better equipped to analyze and solve problems with greater precision and efficiency.
Interpreting Graphs and Tables
Graphs and tables are powerful tools for visualizing and analyzing data. By interpreting these representations correctly, you can gain insights into trends, relationships, and patterns that might not be immediately obvious in raw data. Developing strong skills in reading and understanding graphs and tables is essential for solving problems and making informed conclusions in various scenarios.
Analyzing Data from Graphs

Graphs provide a visual summary of data that helps to identify important trends and features. When interpreting graphs, pay attention to the following elements:
- Axes and Scale: Check the labels and units on the axes to understand the context of the graph.
- Key Features: Look for intercepts, maxima, minima, and asymptotes that can reveal critical information about the function.
- Trends and Patterns: Observe how the graph behaves over different intervals to identify trends or changes in direction.
Reading Information from Tables

Tables offer a structured way of presenting data, often in rows and columns. When interpreting tables, focus on the following points:
- Column Headings: Understand what each column represents and how the data is organized.
- Data Relationships: Compare values across rows or columns to detect any correlations or patterns.
- Trends and Outliers: Look for any unusual values or trends that could indicate significant findings.
By practicing these techniques, you’ll become more adept at extracting meaningful information from both graphs and tables, helping you solve problems more efficiently.
How to Maximize Your Score
Achieving the best possible score requires more than just understanding the material–it involves strategic preparation, effective time management, and smart decision-making during the test. By following a structured approach, you can maximize your performance and approach the test with confidence.
Effective Study Strategies
Begin your preparation by identifying your strengths and weaknesses. Focus your efforts on areas where you need improvement, while also reinforcing your strong points. Here are some strategies to help you study efficiently:
- Practice Regularly: Consistent practice helps reinforce concepts and build problem-solving speed.
- Review Past Mistakes: Analyze mistakes from previous practice sessions to avoid repeating them.
- Use Study Aids: Utilize textbooks, online resources, and review guides to cover a wide range of topics.
- Work with Peers: Collaborate with classmates or study groups to share insights and strategies.
During the Test: Time Management and Strategy

When it comes time to take the test, effective time management is crucial to maximize your score. Here are some tips to manage your time efficiently:
- Allocate Time Wisely: Divide your time according to the difficulty and length of each section.
- Don’t Get Stuck: If you’re unsure about a question, move on and come back to it later. Prioritize questions you know first.
- Double-Check Answers: If time allows, review your answers to ensure accuracy, especially on tricky questions.
By applying these strategies, you can boost your chances of achieving your best possible score, all while managing stress and time effectively during the test.
Importance of Calculators in the Exam
In many assessments, the proper use of calculators plays a critical role in solving complex problems quickly and accurately. A calculator can save valuable time and help you perform calculations that would otherwise be tedious or error-prone. Knowing how to use your calculator effectively can make a significant difference in your overall performance.
Advantages of Using a Calculator
Here are some key benefits of incorporating a calculator into your approach:
- Speed: Calculators can speed up arithmetic and algebraic tasks, allowing you to focus more on problem-solving strategies.
- Accuracy: Using a calculator reduces the chances of making mistakes in complex calculations, especially under time constraints.
- Complex Functions: Certain problems require advanced functions such as derivatives, integrals, or graphing. Calculators can simplify these tasks and make them more manageable.
When and How to Use the Calculator
While calculators are incredibly helpful, it’s important to know when to use them and how to use them effectively:
- Understand the Allowed Functions: Make sure you are familiar with the functions your calculator offers and how they align with the rules of the assessment.
- Don’t Over-Rely: Although calculators are helpful, it’s essential to understand the underlying concepts and not become overly dependent on the tool.
- Practice with Your Calculator: Spend time before the test practicing with your calculator to ensure you are comfortable and familiar with its features.
Types of Calculators Allowed
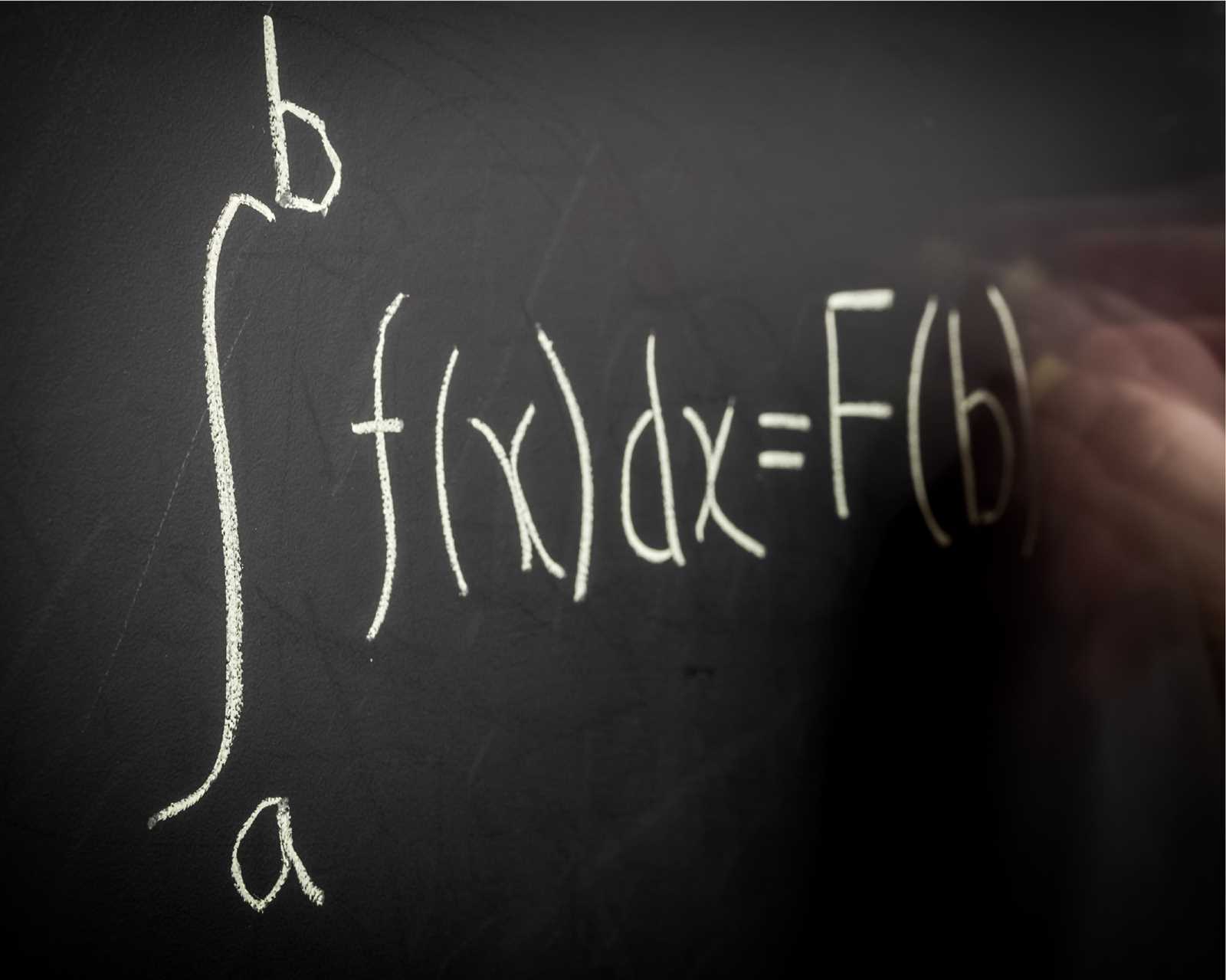
Each assessment may have specific rules about which calculators are allowed. The most common types of calculators include:
| Type of Calculator | Description |
|---|---|
| Basic Calculators | These calculators perform simple arithmetic but lack advanced functions such as graphing or solving equations. |
| Scientific Calculators | These calculators are equipped with advanced functions such as trigonometry, logarithms, and exponentiation. |
| Graphing Calculators | Graphing calculators allow users to graph functions, solve equations, and perform more advanced mathematical operations. |
By understanding the capabilities and limitations of your calculator, you can maximize its effectiveness during the test, allowing you to focus on solving problems efficiently and accurately.
Post-Assessment Review and Reflection
After completing an assessment, taking the time to review your performance is essential for identifying strengths and areas for improvement. Reflecting on your approach to different questions allows you to understand what strategies worked well and where adjustments can be made in the future. This process is crucial for continued growth and better preparation for subsequent challenges.
Engaging in a thorough review helps you to analyze your mistakes, solidify your knowledge, and develop more effective problem-solving techniques for future assessments. It also gives you an opportunity to reinforce key concepts and ensure that your understanding remains clear and accurate.
Steps for Effective Review
To make the most of your post-assessment review, consider the following steps:
- Review Mistakes: Go through each question you struggled with and understand why you made an error. Was it a misunderstanding of the concept, a simple miscalculation, or a time management issue?
- Revisit Concepts: If there were certain topics that caused difficulties, revisit them thoroughly. Study the foundational principles and practice similar problems to reinforce your understanding.
- Analyze Your Approach: Reflect on how you approached each problem. Did you read the instructions carefully? Did you break the problem into manageable parts? Identifying your problem-solving process will help you improve it for the future.
Incorporating Feedback
If you have access to feedback, whether from a teacher, tutor, or peers, use it constructively. Feedback can provide valuable insights into how you can enhance your approach and better prepare for similar tasks. Incorporating this feedback into your study routine can help you address any lingering weaknesses.
By taking the time to analyze your performance and make necessary adjustments, you’ll be better equipped for future challenges. A thoughtful post-assessment reflection can not only improve your skills but also enhance your confidence and readiness for upcoming assessments.
Staying Calm and Confident During the Test
Maintaining composure and confidence throughout a challenging assessment is key to performing at your best. Often, nervousness can cloud your judgment and hinder your ability to think clearly, so it’s important to cultivate strategies that help you stay relaxed and focused. By preparing mentally and physically in advance, you can approach the task with a calm mindset and a positive attitude.
Confidence doesn’t just come from knowledge–it’s also about trusting your abilities and staying composed under pressure. During the assessment, managing stress and anxiety is crucial for staying on track and making thoughtful decisions. With the right techniques, you can maintain a clear focus, even when faced with complex or unexpected questions.
Techniques for Staying Calm
Here are some strategies to help you maintain a calm and collected mindset during the assessment:
- Deep Breathing: Take a few slow, deep breaths to calm your mind and reduce anxiety. This will help lower your stress levels and improve focus.
- Positive Visualization: Before you begin, visualize yourself successfully completing the test. Imagine yourself moving through each question with confidence.
- Focus on One Question at a Time: Instead of worrying about the entire assessment, focus on tackling each question individually. Breaking it down can make it seem more manageable.
Building Confidence Before the Test
Building your self-assurance doesn’t start on the day of the assessment. To feel confident during the test, consistent preparation is key. Regular practice, reviewing key concepts, and identifying your strengths and areas for growth will ensure you feel more prepared. When you’re confident in your abilities, you can approach the task without hesitation.
Ultimately, staying calm and confident is about adopting the right mindset. Remember, you’ve put in the work, and you are capable of handling the challenge. Trust your preparation, take it one step at a time, and give yourself credit for the effort you’ve made.