
Preparing for a challenging assessment in advanced mathematics requires a clear understanding of the key topics and strategies to succeed. The test offers a comprehensive evaluation of problem-solving abilities, theoretical knowledge, and practical application of mathematical concepts. Mastering the core principles and developing strong analytical skills are essential to perform well.
Focused practice and reviewing detailed solutions to complex problems can help solidify your grasp of important ideas. Identifying recurring problem types and learning effective methods for approaching them can boost your confidence and efficiency. By focusing on common patterns and applying mathematical rules systematically, you can enhance your problem-solving capabilities.
Through thorough preparation, learners can better handle the pressures of time constraints and the difficulty of the questions. Consistent practice with diverse problems, alongside targeted review, will help you approach each challenge with a clear and structured method. Aim to understand the underlying concepts deeply rather than simply memorizing steps for solving problems.
AP Calculus AB Exam 4 Solutions
In this section, we will explore the step-by-step solutions to the key problems from the fourth assessment in the AP Calculus AB course. This guide will help you understand the approach to solving complex questions and ensure you grasp the essential concepts that are frequently tested.
Understanding the method behind each solution is crucial for mastering the material. Each problem in the assessment is designed to test specific skills, such as problem-solving techniques, mathematical reasoning, and the ability to apply formulas correctly. Below is a breakdown of the most commonly encountered problem types and their solutions:
- Derivatives of Functions – Learn the techniques for finding the rate of change of various functions, including trigonometric, exponential, and logarithmic functions.
- Integrals – Explore how to evaluate the area under curves and apply integration rules to solve definite and indefinite integral problems.
- Limits and Continuity – Study how to determine the behavior of functions at critical points and handle indeterminate forms.
- Application of the Fundamental Theorem – Understand how to connect the process of differentiation with integration to solve more complex problems.
By reviewing these solutions, you can improve your ability to approach similar problems on future assessments. Pay special attention to the reasoning and methods behind each step, as these are the skills that will lead to a successful result.
Additionally, practicing with multiple examples and reviewing your work can help solidify these techniques in your memory. Mastery of these concepts is essential not only for exams but also for future advanced studies in mathematics.
Overview of AP Calculus AB Exam 4
The fourth assessment in the AP Calculus AB course is designed to evaluate your understanding and application of key mathematical concepts. It tests your ability to solve a variety of problems related to derivatives, integrals, and the fundamental theorems of calculus. The questions are intended to challenge your problem-solving skills and mathematical reasoning.
This section covers a wide range of topics, each testing different aspects of your knowledge. It is important to familiarize yourself with the types of questions typically asked and the strategies for tackling them effectively. Below is an overview of the major topics you will encounter:
- Rates of Change – Focuses on understanding how quantities change over time or space, often involving the derivative of a function.
- Definite and Indefinite Integrals – Tests your ability to calculate the area under curves, as well as evaluating integrals of various functions.
- Applications of Derivatives – Includes problems related to optimization, related rates, and analyzing the behavior of functions.
- Fundamental Theorem of Calculus – Assesses your ability to connect integration and differentiation in solving problems.
Success in this assessment requires a solid understanding of these core topics and the ability to apply them in various scenarios. Reviewing key concepts and practicing different problem types will prepare you for the challenges ahead.
Key Concepts Tested in Exam 4
The fourth assessment focuses on fundamental principles that are essential for solving a variety of mathematical problems. It is designed to test your ability to apply theoretical concepts to real-world situations, requiring both problem-solving skills and a deep understanding of core ideas.
The main concepts evaluated in this section include:
- Derivative Applications – The ability to find and interpret rates of change, as well as solving problems involving related rates, motion, and optimization.
- Definite and Indefinite Integration – Understanding how to calculate areas under curves, find antiderivatives, and apply integration rules to solve problems.
- Limits and Continuity – Evaluating the behavior of functions as they approach specific values or infinity, and determining whether functions are continuous.
- Fundamental Theorem of Calculus – Connecting differentiation and integration, using the theorem to solve problems involving both processes.
Mastering these key concepts is crucial for success. They provide the foundation for tackling complex problems and applying mathematical reasoning effectively. A solid grasp of these principles will enable you to approach a wide variety of questions with confidence.
Solving Differential Equations in Exam 4
Solving differential equations is a key component of the fourth assessment, where you will be required to find solutions to equations that describe rates of change. These types of problems test your ability to apply mathematical methods to understand and solve dynamic systems.
Types of Differential Equations

In this section, you will encounter various forms of differential equations, including separable equations and first-order linear equations. Solving these requires different strategies, such as:
- Separation of Variables – Rearranging terms to isolate variables on opposite sides of the equation before integrating both sides.
- Integrating Factor Method – Using an integrating factor to simplify and solve first-order linear equations.
General Strategy for Solving
When approaching a differential equation, it’s important to follow a systematic process. First, identify the type of equation you are dealing with. Next, choose the appropriate solving technique and carefully apply it step-by-step. Pay attention to initial conditions when they are provided, as they help you find a specific solution rather than a general one.
By practicing these techniques, you will be better equipped to handle the more complex problems that may appear on the test. A strong understanding of these methods is essential for success in solving differential equations.
Understanding Limits and Continuity
In this section, you will explore the fundamental concepts of limits and continuity, which form the foundation for understanding how functions behave as they approach specific values. These concepts are essential for analyzing the behavior of functions, especially when dealing with indeterminate forms and discontinuities.
What Are Limits?
Limits describe the behavior of a function as it approaches a particular point. Understanding limits allows you to determine the value a function approaches even if it is not explicitly defined at that point. The concept is crucial for analyzing the smoothness of functions and understanding their overall behavior in various contexts.
Continuity of Functions

A function is continuous if it does not have any interruptions, jumps, or holes at a particular point. Continuity ensures that the function behaves predictably as its input changes. If a function is continuous, you can confidently calculate its values at any point within its domain.
| Condition for Continuity | Explanation |
|---|---|
| The function is defined at the point | The function must have a value at the point in question. |
| Limit exists at the point | The left-hand limit and right-hand limit must be equal at the point. |
| The limit equals the function value | The function’s value at the point must match the limit as the function approaches that point. |
By mastering the concepts of limits and continuity, you will be able to analyze and solve problems more effectively, ensuring you understand the behavior of functions in different scenarios. These ideas are foundational for tackling more complex problems in calculus and related fields.
Exam Strategies for Success
Success in any rigorous test requires more than just understanding the material; it involves effective strategies for managing time, reducing errors, and optimizing performance. The following strategies can help you approach the test with confidence and improve your chances of achieving your desired result.
To maximize your performance, it is important to have a clear plan of action before, during, and after the assessment. Focusing on efficient problem-solving techniques, managing stress, and staying organized are key to navigating challenging questions effectively.
| Strategy | Explanation |
|---|---|
| Review Key Concepts | Before the test, focus on understanding the most frequently tested topics. Make sure you’re familiar with common problem types and their solutions. |
| Time Management | Allocate a specific amount of time for each section. Don’t get stuck on any one question for too long. Move on and return to difficult problems if needed. |
| Read Questions Carefully | Take time to understand what the question is asking. Pay attention to specific instructions and details, such as units or limits of integration. |
| Show Your Work | Write out all the steps in your solution, even if you can solve the problem mentally. This helps you avoid mistakes and makes it easier to earn partial credit. |
| Stay Calm Under Pressure | Practice relaxation techniques, such as deep breathing, to maintain focus during the test. Stress can cloud your judgment, so stay calm and confident. |
By implementing these strategies, you can reduce the pressure of the test and approach it in a more structured and confident way. Preparation, time management, and clarity in your approach are crucial elements in maximizing your performance.
Graphing Techniques for Exam 4
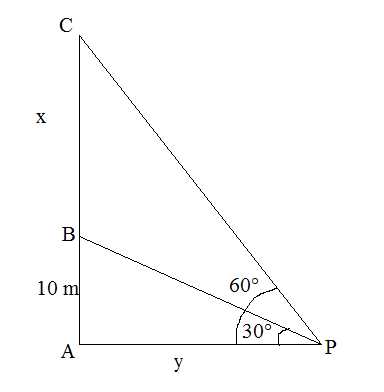
Graphing is a powerful tool for understanding the behavior of functions. Whether you are dealing with polynomial functions, rational functions, or trigonometric expressions, being able to represent these functions visually will help you gain insights into their key characteristics. Mastering effective graphing techniques will enable you to quickly identify important features such as intercepts, asymptotes, and turning points, all of which are critical for solving problems efficiently during the assessment.
In this section, we will explore essential strategies for graphing different types of functions and how to use these methods to simplify complex problems. The following table highlights key graphing techniques that will help you approach each function systematically:
| Technique | Explanation |
|---|---|
| Identifying Key Points | Start by finding important points such as x- and y-intercepts, local maxima, and minima. These points provide a foundation for sketching the graph accurately. |
| Asymptotes and End Behavior | Examine the behavior of the function at the limits of the graph. Vertical asymptotes indicate points where the function approaches infinity, while horizontal asymptotes show the long-term behavior of the function as x approaches infinity. |
| Using Symmetry | If the function is even or odd, use symmetry to reduce the effort needed to graph it. Even functions exhibit symmetry about the y-axis, while odd functions have symmetry about the origin. |
| Plotting Critical Points | Find the derivative of the function to determine critical points where the function changes direction (increases to decreases or vice versa). These points often correspond to local minima or maxima. |
| Consider Discontinuities | Pay attention to discontinuities, such as holes or jumps in the graph. These can occur when a function is not defined at certain points or when there are vertical asymptotes. |
By incorporating these graphing techniques into your problem-solving process, you will be able to more effectively analyze and visualize the behavior of functions, making it easier to draw accurate conclusions and solve problems with confidence during the test.
Common Mistakes to Avoid on Exam 4
When taking a challenging test, it’s easy to make errors that can cost valuable points. Even if you understand the material, simple mistakes can arise from rushing, misinterpreting questions, or overlooking important details. In this section, we will highlight common pitfalls and offer strategies for avoiding them to ensure that you perform at your best.
Being aware of these common mistakes will help you stay focused and minimize the risk of errors during the assessment. Below are some key areas where students often go wrong:
Misreading Instructions
One of the most frequent errors students make is misinterpreting the instructions in the questions. Always read each question carefully and ensure you understand exactly what is being asked before proceeding. For example, a question might ask for a “simplified” expression, but if you fail to notice this, you might leave your answer in an expanded or factored form.
Overlooking Units and Constants
Another common mistake involves forgetting to include units in your final answers or neglecting constants when performing operations. Whether you’re solving for velocity, distance, or time, always double-check that your final answer includes the correct units. Additionally, ensure you don’t miss any constants in formulas, as omitting them can lead to incorrect solutions.
By keeping these mistakes in mind and staying vigilant throughout the test, you can avoid many common errors and boost your chances of achieving a higher score. Attention to detail and careful reading of each question are key to success.
Step-by-Step Solutions for Exam 4
Approaching complex problems methodically is essential for achieving accurate results. In this section, we will break down some of the most common types of questions into simple, logical steps. This approach will help you understand how to tackle each problem systematically, ensuring you don’t overlook important details and can maximize your performance.
By following a step-by-step process, you can stay organized and confident as you work through each question. Below is a general approach to solving common problems:
- Understand the Problem – Begin by carefully reading the problem to ensure you understand what is being asked. Identify the key variables and what needs to be solved for.
- Set Up the Equation – Once you know what the problem is asking, set up the relevant equation or system. Make sure all terms are included, and all known values are properly accounted for.
- Simplify the Equation – Before proceeding, simplify the equation if possible. Eliminate unnecessary terms or factors, and combine like terms to make the problem easier to solve.
- Apply the Appropriate Method – Whether it’s substitution, elimination, integration, or any other method, apply the correct technique for the type of problem you’re solving.
- Check Your Work – After finding the solution, go back and verify each step. Ensure that your calculations are correct and that your solution answers the original question.
This approach not only helps you solve problems accurately but also ensures you remain organized under timed conditions. Practicing these steps will build confidence and reduce the chances of making errors in the final solution.
How to Prepare for AP Calculus AB
Effective preparation for a challenging test requires a combination of time management, thorough understanding of the material, and consistent practice. Developing a strategy for review, honing problem-solving skills, and strengthening your grasp of key concepts will help you approach the assessment with confidence. In this section, we will explore practical steps to guide you through the preparation process.
Develop a Study Plan
Planning your study sessions is essential for efficient preparation. A structured approach allows you to cover all necessary topics without feeling overwhelmed. Here are some strategies to consider:
- Set a Schedule – Break your study time into manageable blocks, focusing on different topics each day. Make sure to leave time for review and practice.
- Prioritize Weak Areas – Identify the areas where you struggle most and spend extra time reinforcing your understanding in those areas.
- Stay Consistent – Regular study sessions, even for shorter periods, are more effective than cramming at the last minute.
Review Key Topics
To ensure you’re ready for all aspects of the test, it’s important to revisit the major concepts and techniques covered throughout the course. Focus on the following key areas:
- Fundamental Theorems and Properties – Review the core theorems, their proofs, and how they are applied to solve problems.
- Problem-Solving Techniques – Practice using various methods, such as substitution, integration, and optimization, to solve different types of problems.
- Graphing Functions – Be comfortable with interpreting and analyzing graphs of functions, as this is a key skill for many questions.
By following a structured plan and reviewing essential topics regularly, you will improve your knowledge and skills, putting yourself in the best position for success on the assessment.
Important Formulas for Exam 4
Having a solid understanding of key formulas is crucial for solving complex problems efficiently. These formulas serve as the foundation for tackling a wide range of questions. In this section, we will outline the most important formulas that are commonly used and will help you solve problems with greater ease and accuracy.
Ensure that you are familiar with these formulas, as they are frequently tested and play a central role in various types of questions. Below is a list of the essential formulas you should be comfortable with:
- Power Rule for Derivatives
If f(x) = x^n, then f'(x) = n * x^(n-1).
- Chain Rule
If y = g(f(x)), then dy/dx = g'(f(x)) * f'(x).
- Product Rule
If y = u(x) * v(x), then dy/dx = u'(x) * v(x) + u(x) * v'(x).
- Quotient Rule
If y = u(x) / v(x), then dy/dx = (v(x) * u'(x) – u(x) * v'(x)) / (v(x))^2.
- Integration by Parts
If u(x) and v(x) are differentiable, then ∫ u(x) * v'(x) dx = u(x) * v(x) – ∫ v(x) * u'(x) dx.
- Fundamental Theorem of Calculus
If F is the antiderivative of f, then ∫ from a to b of f(x) dx = F(b) – F(a).
By committing these formulas to memory and practicing their application, you will enhance your ability to solve problems quickly and effectively. These formulas are fundamental to the skills required for the assessment and should be mastered in order to perform well.
Review of Integration Problems
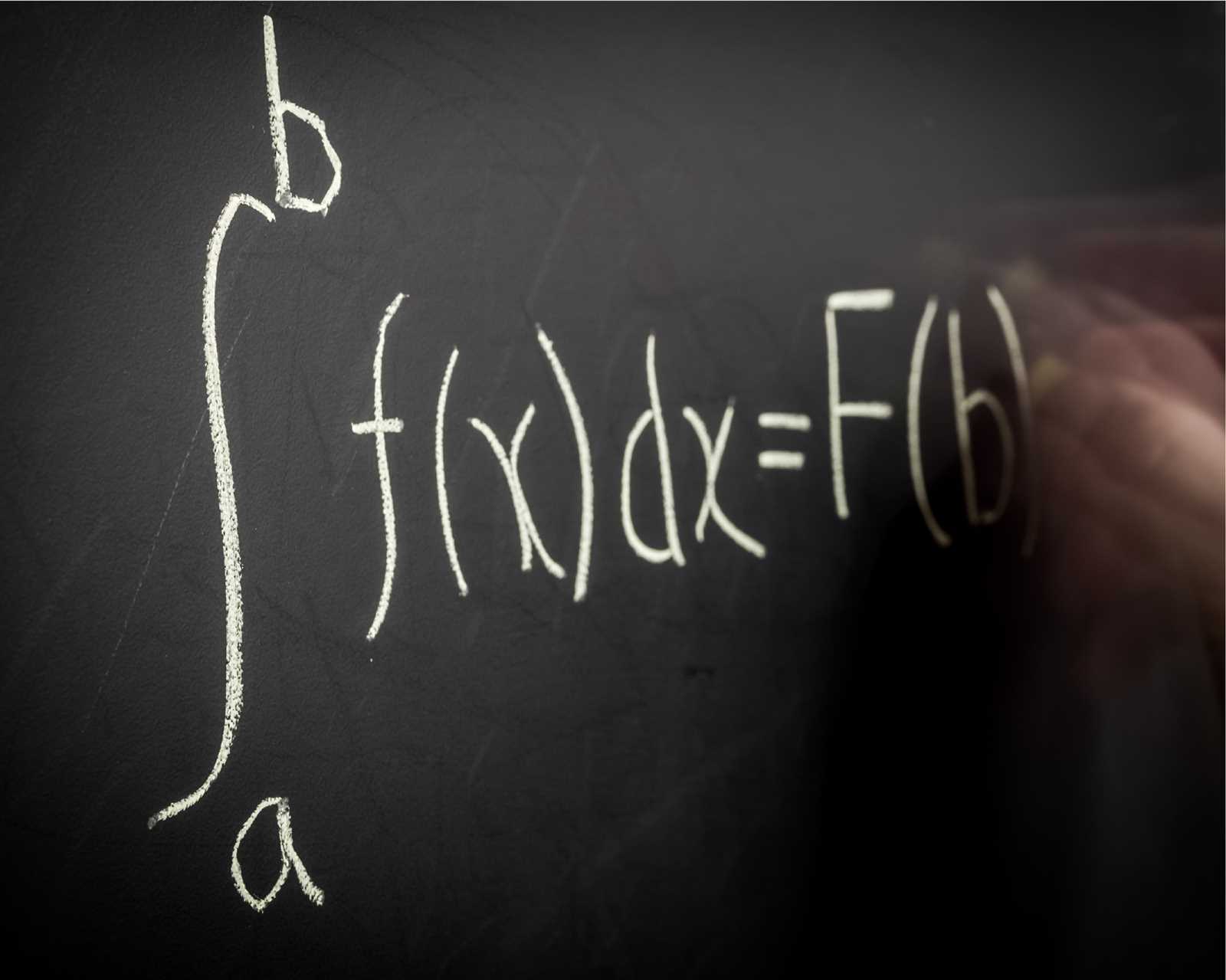
Mastering integration is essential for solving a wide range of mathematical problems. Whether you’re tasked with finding the area under a curve, solving real-world problems, or evaluating complex expressions, having a strong grasp of integration techniques is crucial. This section reviews the most common types of integration problems that are frequently encountered and provides useful methods for solving them efficiently.
From basic antiderivatives to advanced techniques like integration by parts and substitution, understanding the core strategies is key to achieving success. Below are some of the fundamental approaches and examples of integration problems that often appear in tests:
- Basic Power Rule
For any power of x, the integral is calculated as ∫ x^n dx = (x^(n+1))/(n+1), where n ≠ -1.
- Integration by Substitution
This technique is useful when an integral contains a composite function. It involves replacing a part of the integrand with a new variable. For example, ∫ f(g(x)) * g'(x) dx becomes ∫ f(u) du, where u = g(x).
- Integration by Parts
This method applies when the integrand is a product of two functions. The formula is ∫ u * v dx = u * ∫ v dx – ∫ (u’ * ∫ v dx).
- Trigonometric Integrals
Involves integrating functions that include trigonometric expressions. For example, ∫ sin(x) dx = -cos(x) or ∫ cos(x) dx = sin(x).
- Partial Fractions
This technique breaks a rational function into simpler fractions to make integration easier. For example, ∫ (1/(x^2 + 1)) dx = arctan(x).
- Definite Integrals
These integrals involve calculating the area under a curve over a specific interval. The formula is ∫ from a to b f(x) dx = F(b) – F(a), where F is the antiderivative of f.
By practicing these different methods and solving integration problems regularly, you’ll gain confidence in handling more complex questions. Remember that some problems may require a combination of techniques, so always be ready to apply multiple strategies to reach the solution.
Practice Questions for Exam 4
Practicing problem sets is one of the most effective ways to prepare for any assessment. In this section, we provide a variety of problems that cover key concepts and techniques often tested in the final part of the course. These practice questions are designed to help you refine your skills, identify areas for improvement, and gain confidence in solving a range of mathematical challenges.
By working through these problems, you’ll not only reinforce your understanding of the material but also develop strategies for tackling similar questions during the actual test. The following questions span various topics and difficulty levels, ensuring a comprehensive review:
- Question 1: Find the area under the curve y = 3x^2 + 2x – 1 from x = 1 to x = 4.
- Question 2: Solve the differential equation dy/dx = 5x^3 – 2x.
- Question 3: Evaluate the integral ∫ (4x^3 – 2x^2 + 7) dx.
- Question 4: Using substitution, evaluate ∫ (2x * sqrt(1 + x^2)) dx.
- Question 5: Find the limit of f(x) = (x^2 – 4)/(x – 2) as x → 2.
- Question 6: Determine whether the function f(x) = 1/x is continuous at x = 0.
- Question 7: Solve the integral using integration by parts: ∫ x * e^x dx.
- Question 8: Find the derivative of f(x) = ln(x^2 + 1).
- Question 9: Determine the area between the curves y = x^2 and y = x + 2.
- Question 10: Evaluate the definite integral ∫ from 0 to 2 (3x^2 – x) dx.
These questions cover a broad range of techniques, from integration and differentiation to limits and continuity. Be sure to attempt each one, and practice working through different methods of solving similar types of problems. After completing these, check your solutions against reliable references or solutions guides to ensure you’re on the right track.
Time Management Tips During the Exam
Effective time management is crucial when tackling any challenging assessment. Properly allocating your time ensures that you can address all sections of the test with adequate focus and accuracy. In this section, we offer valuable strategies to help you maximize your performance by efficiently managing the available time.
Prioritize and Plan

Start by reviewing the entire test quickly before diving into individual problems. This will give you a sense of what to expect and help you determine which sections might require more time. Prioritize questions that you find easier or are more familiar with to build momentum. Then, tackle more complex problems later, once you’ve gained confidence and familiarity with the test format.
Set Time Limits for Each Section
Divide your total time according to the number of questions or sections. Set a mental or written timer for each section, and aim to finish each part within the allotted time. For example, if you have 60 minutes and 20 questions, aim to spend no more than 3 minutes per question. If you get stuck on a problem, move on and return to it later. This approach helps prevent wasting time on a single question that might slow you down.
Remember to leave a few minutes at the end to review your answers. Double-check your calculations and make sure you’ve answered all the questions. Efficient time management allows you to avoid feeling rushed and ensures you complete the test to the best of your ability.
Analyzing Functions and Derivatives
Understanding the behavior of functions and their derivatives is essential for solving a wide range of mathematical problems. By analyzing a function’s rate of change, we can determine important characteristics such as increasing or decreasing intervals, local extrema, and concavity. In this section, we focus on methods to effectively interpret and work with functions and their derivatives.
Identifying Critical Points
Critical points are where the function’s derivative is zero or undefined. These points are crucial for determining where a function changes direction, and they often indicate potential local maxima or minima. To find critical points, start by taking the derivative of the function and setting it equal to zero. Solve for the variable to locate the potential critical points.
Understanding Concavity and Inflection Points
Concavity refers to the direction in which a function curves. A function is concave up if its slope is increasing and concave down if its slope is decreasing. Inflection points occur where a function changes concavity. To analyze concavity, calculate the second derivative. If the second derivative is positive, the function is concave up; if it’s negative, the function is concave down. Inflection points happen when the second derivative equals zero and changes sign.
By mastering these concepts, you’ll be able to gain deeper insights into the behavior of functions, which is fundamental for solving both theoretical and practical problems efficiently.
Additional Resources for Exam Preparation

Preparing for a challenging test requires more than just practice problems. Utilizing a variety of supplementary materials can significantly enhance your understanding and confidence. In this section, we explore several resources that can help you strengthen your skills and optimize your study approach.
Online Platforms and Tutorials
Online learning platforms provide access to a wide array of resources, including instructional videos, practice questions, and interactive tools. Websites like Khan Academy, Coursera, and YouTube offer detailed explanations of key topics, along with strategies for problem-solving. These platforms often include quizzes and assignments that allow you to test your knowledge and track your progress.
Textbooks and Practice Guides
Textbooks are an invaluable resource for in-depth understanding, offering step-by-step explanations of complex concepts. Additionally, specialized practice guides can help you prepare for specific sections of the test. These guides often contain worked-out examples, multiple practice questions, and answer keys that enable self-assessment. Many publishers also offer online resources or companion websites that provide further exercises and support.
By incorporating these additional resources into your study routine, you can deepen your comprehension and tackle the material from various angles, ultimately improving your performance when it counts the most.