Calculus Final Exam with Complete Answers and Solutions

Preparing for a comprehensive assessment in higher-level mathematics requires a deep understanding of key concepts and the ability to apply them effectively. This section will guide you through essential strategies and techniques to succeed when tackling complex problems. By mastering the core principles and honing problem-solving skills, you can approach your assessment with confidence.

Thorough practice is vital to reinforce your knowledge and ensure quick recall under pressure. Whether it’s evaluating intricate expressions, solving challenging equations, or applying various mathematical methods, consistent preparation will strengthen your grasp on the subject.

In this guide, you’ll find step-by-step instructions and problem-solving approaches designed to help you navigate through the toughest sections of your assessment. Stay focused, manage your time wisely, and practice regularly to achieve the best results.

Essential Tips for Success in Your Math Assessment

Achieving success in an advanced mathematics assessment requires more than just understanding the theory. It involves knowing how to approach problems efficiently, manage time effectively, and apply the right strategies for each type of question. Preparation is key to tackling the more complex parts of the subject, and a solid plan will ensure that you can perform at your best.

Master the Core Concepts

Before diving into practice problems, make sure you have a solid understanding of the foundational concepts. These form the basis for solving more intricate problems and help you identify patterns. Spend time reviewing key formulas, theorems, and methods that are most commonly tested. Understanding the “why” behind each method will allow you to apply them more effectively.

Practice Under Timed Conditions

Repetition is crucial for building confidence. Work through problems regularly and try to simulate test conditions by timing yourself. This will not only help you get used to the pressure but also improve your speed and accuracy. Regular practice will help you identify areas that need improvement and refine your problem-solving techniques.

Understanding Key Mathematical Concepts

To excel in any advanced mathematical assessment, a solid grasp of the core principles is essential. These fundamental concepts serve as the building blocks for more complex problem-solving. A deep understanding of each principle allows you to recognize patterns, apply strategies correctly, and tackle even the most challenging questions.

Limits and Continuity

Limits form the foundation of many techniques used in advanced mathematics. Understanding how functions behave as they approach a specific value is crucial for solving a wide range of problems. Familiarize yourself with the different types of limits, such as one-sided limits, infinite limits, and limits at infinity. Additionally, recognize the importance of continuity in ensuring that functions behave predictably over intervals.

Derivatives and Integrals

Derivatives represent the rate of change, while integrals are used to calculate areas under curves or the accumulation of quantities. Mastering both of these concepts is essential, as they are the core methods for analyzing and solving problems related to motion, growth, and optimization. Practice working with different types of derivatives and integrals, such as power, product, and chain rules, to build a strong foundation.

How to Approach Problems Effectively

Successfully solving mathematical problems under pressure requires a strategic approach. Knowing how to break down complex questions into manageable steps can help you focus on finding the correct solutions more efficiently. By following a clear method, you’ll be able to stay organized and reduce the likelihood of making mistakes during the assessment.

Start by carefully reading each question to ensure you understand what is being asked. Identify key information and underline or highlight important details. If the problem involves multiple steps, jot down a brief outline of the approach you plan to take. This will help you stay focused and avoid missing crucial parts of the problem.

Next, tackle the easiest questions first. This builds confidence and allows you to secure marks early on. Once you’ve completed the simpler problems, you can dedicate more time to the more complex ones. If you encounter a particularly challenging question, don’t panic–move on and return to it later with a fresh perspective. Time management is critical, so be sure to pace yourself throughout the process.

Common Mistakes to Avoid During the Test

While preparing for and taking a complex mathematics test, it’s easy to make avoidable errors that can cost valuable points. Recognizing these common pitfalls and taking steps to avoid them can significantly improve your performance. By being mindful of these mistakes, you can approach the test with more confidence and accuracy.

Rushing Through Questions

One of the most frequent mistakes students make is rushing through questions without fully understanding what’s being asked. It’s essential to carefully read each problem and identify all key components before jumping into a solution. Avoid the temptation to move too quickly, especially when you feel confident about a question. Rushing often leads to overlooked details or misinterpreted instructions.

Neglecting to Check Work

Forgetting to verify your calculations can result in simple arithmetic mistakes.
Skipping back to check the steps can cause missed opportunities for corrections.
Double-checking helps to identify any inconsistencies and prevents errors from affecting your score.

Overlooking Time Management

Failing to allocate time wisely can lead to incomplete answers or rushed solutions.
Be aware of how much time you’re spending on each question. It’s crucial to balance speed and accuracy.
Ensure that you have enough time to tackle all questions and leave room for review at the end.

Step-by-Step Guide to Solving Mathematical Problems

When faced with complex mathematical problems, breaking them down into smaller, manageable steps is essential for finding the correct solutions. A systematic approach helps prevent confusion and ensures that no critical part of the problem is overlooked. By following a structured method, you can tackle even the most challenging questions with confidence.

Analyze the Problem

Before attempting to solve the problem, take a moment to thoroughly read and understand it. Identify the known values, the unknowns, and what the problem is asking you to find. Underline or highlight key information that may be useful in your calculations. This initial step ensures that you don’t overlook any important details and sets the stage for the next steps.

Break It Down and Solve Step-by-Step

Once you’ve analyzed the problem, break it down into smaller parts. For example, if the problem involves multiple steps or concepts, address each one individually. Work through each step slowly and methodically, showing all your calculations. This approach not only helps you stay organized but also makes it easier to identify and correct any mistakes along the way.

Breaking Down Complex Integrals

Solving intricate integrals can be a daunting task, but approaching them methodically can make the process more manageable. A clear step-by-step strategy allows you to break down complex expressions and handle them effectively. By recognizing key patterns and applying appropriate techniques, you can simplify even the most challenging integrals.

Recognizing Common Patterns

Before starting the calculation, look for familiar patterns that can help simplify the integral. Common techniques like substitution or integration by parts are useful for transforming a complicated integral into a more straightforward one. Identifying these patterns early on can save time and reduce the complexity of the problem.

Check for opportunities to apply u-substitution for integrals involving composite functions.
Look for products of functions where integration by parts might be applicable.
Consider trigonometric identities or exponential forms that may simplify the integral.

Breaking the Integral into Parts

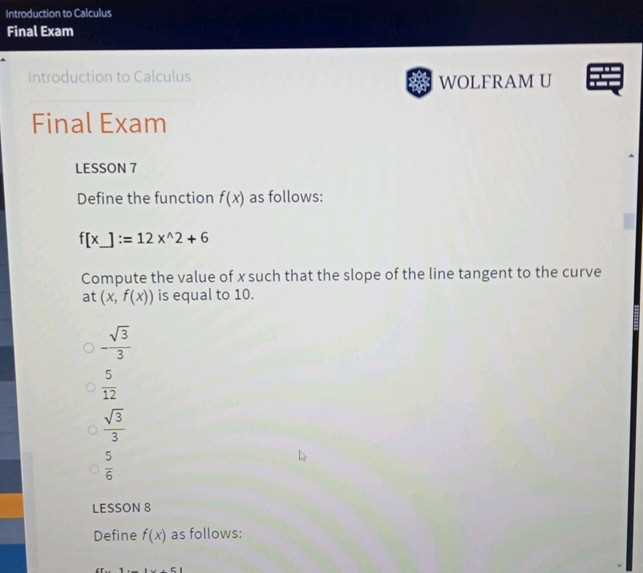
If the integral is still difficult to solve in one step, try splitting it into smaller, more manageable components. This can often make the process easier by addressing each part of the function separately. By breaking down the integral, you not only make it more accessible but also gain better control over the solution process.

Split the integral into simpler functions if possible.
Apply standard rules for integrating polynomials, exponentials, or trigonometric functions.
Recombine the parts after solving each individual segment.

Mastering Derivatives for the Assessment

Understanding the concept of derivatives is crucial for tackling a wide range of problems that involve rates of change and slopes. Whether you’re dealing with polynomials, rational functions, or trigonometric expressions, mastering the rules and techniques for finding derivatives will be key to your success. With practice, you’ll be able to differentiate complex functions quickly and accurately.

Key Rules to Remember

There are several fundamental rules that you’ll need to apply frequently when working with derivatives. These rules simplify the process and help you handle a variety of functions. Make sure to commit them to memory and understand how to use them in different situations.

Power Rule: For any function of the form f(x) = x^n, the derivative is f'(x) = n*x^(n-1).
Product Rule: For two functions u(x) and v(x), the derivative of their product is u'(x)v(x) + u(x)v'(x).
Quotient Rule: For a quotient of functions u(x)/v(x), the derivative is (v(x)u'(x) – u(x)v'(x)) / [v(x)]².
Chain Rule: For composite functions, use f'(g(x)) = f'(g(x)) * g'(x).

Practice and Application

To truly master derivatives, you must practice solving a wide range of problems. Start with simpler functions to build your confidence, then gradually move on to more complex expressions that involve multiple rules. Regular practice will help reinforce these concepts and improve your speed during the assessment.

Begin with basic polynomial and trigonometric functions to get comfortable with the rules.
Progress to more complex functions, such as products, quotients, and composite functions.
Work through a variety of problems to apply different rules in combination.
Review your work to ensure you understand the reasoning behind each step.

Preparing for Limits and Continuity Questions

When approaching questions that involve the behavior of functions as they approach specific values, it’s essential to understand the underlying concepts of limits and continuity. These topics often form the basis for more advanced problems and are critical for evaluating the behavior of functions at specific points or over intervals. Proper preparation involves familiarizing yourself with the rules, techniques, and common scenarios where limits and continuity are tested.

Key Concepts to Review

To effectively tackle questions on limits and continuity, it’s important to focus on a few core concepts. Understanding how to compute limits in different situations and recognizing when a function is continuous are fundamental skills. Below is a summary of important topics that will help in preparation:

Topic	Key Points
Limits at Specific Points	Evaluate the behavior of a function as it approaches a certain value. Be prepared to apply direct substitution, factoring, or rationalization methods.
Limits at Infinity	Understand horizontal asymptotes and how functions behave as they approach infinity. Pay attention to polynomial, exponential, and rational functions.
Continuity	Check if a function is continuous at a point by ensuring that the limit exists and matches the function’s value at that point.

Common Techniques and Strategies

When solving problems involving limits and continuity, there are several techniques and strategies you should apply based on the given situation:

Direct Substitution: When possible, substitute the value directly into the function to evaluate the limit.
Factoring: Factor complex expressions to simplify the limit calculation, particularly when dealing with indeterminate forms like 0/0.
L’Hopital’s Rule: Use this rule for limits involving indeterminate forms like 0/0 or ∞/∞.
Piecewise Functions: Carefully evaluate limits and check the continuity of piecewise functions at the transition points.

How to Solve Differential Equations Quickly

Solving differential equations efficiently requires understanding the different methods and techniques that can simplify complex problems. Whether you’re dealing with separable, linear, or higher-order equations, recognizing the right approach can save you time and effort. With practice, you can become proficient in solving these equations quickly, even under time constraints.

The key to solving differential equations swiftly is to break them down into manageable steps and apply the appropriate methods. For example, you can use separation of variables for equations that allow it, or integrate factors for linear equations. Developing a systematic approach to identifying the type of differential equation will help you choose the most effective solution strategy.

Common Techniques for Quick Solutions

Here are some widely used methods that can help you solve differential equations efficiently:

Separation of Variables: Useful for equations where both sides can be expressed as a product of functions of one variable each.
Integrating Factor Method: Commonly applied to linear first-order equations. This method helps simplify the equation into an exact form for easy integration.
Homogeneous Equations: For equations where the right-hand side is a function of the dependent variable and its derivatives, use substitution to simplify and solve.
Characteristic Equation: For higher-order linear differential equations, use the characteristic equation to find the roots and determine the general solution.

Practice Makes Perfect

The more you practice solving different types of equations, the more familiar you will become with which methods to use. Start with simpler problems and gradually tackle more complex ones. Over time, you will be able to identify the type of equation at a glance and apply the most efficient solution method quickly.

Tips for Tackling Multivariable Calculus

When dealing with problems that involve multiple variables, it’s important to approach them systematically. Understanding the relationships between the variables and how they interact can make solving these problems much more manageable. Whether you’re dealing with partial derivatives, gradients, or multiple integrals, the key is to develop a clear and consistent method for approaching each type of problem.

In multivariable problems, the complexity arises from the need to handle more than one independent variable at a time. This requires a deeper understanding of how functions change in multiple directions. By breaking down the problem into smaller, more focused steps, you can reduce the complexity and arrive at a solution more efficiently.

Focus on Key Concepts

To effectively solve problems in this area, there are several core concepts to master. Familiarity with these concepts will help you identify the right approach for each problem.

Partial Derivatives: Learn how to differentiate functions of multiple variables with respect to one variable, while holding others constant.
Gradient and Directional Derivatives: Understand how to calculate the gradient of a function and how it relates to the rate of change in different directions.
Multiple Integrals: Be prepared to evaluate integrals over regions in two or three dimensions, applying techniques like changing the order of integration.

Practice and Visualization

One of the most effective ways to build confidence in this area is through consistent practice and visualization. Drawing graphs, visualizing surfaces and curves, and working through practice problems will help you internalize the concepts. Additionally, using tools like contour plots and three-dimensional graphs can aid in understanding the spatial relationships between variables and functions.

Reviewing Integration by Parts and Substitution

Two essential techniques for solving integrals are integration by parts and substitution. Both methods simplify complex integrals by breaking them down into more manageable parts. Understanding when and how to apply each technique is crucial for solving integrals effectively and efficiently. By mastering these methods, you can handle a wide range of integration problems, from simpler to more advanced ones.

Integration by parts is particularly useful when the integrand is a product of two functions. This method leverages the product rule for differentiation, and by applying it in reverse, you can simplify the integral. On the other hand, substitution is ideal when an integral contains a composite function. By changing variables to simplify the integrand, substitution can turn a complicated integral into a more straightforward one.

Integration by Parts

When using integration by parts, you apply the formula:

∫ u dv = uv – ∫ v du

Here, you choose parts of the integrand to set as u and dv, then differentiate u and integrate dv. The key is to select u and dv wisely so that the resulting integral is simpler.

Substitution Method

Substitution is a powerful tool when you encounter integrals with composite functions. The general strategy is to choose a substitution that simplifies the integrand. For example, if the integral contains a function and its derivative, substitution can eliminate the need for integration by parts.

After choosing a substitution, make sure to adjust the limits of integration or the differential accordingly. This will turn the complex integral into one that is easier to solve, often reducing it to a simple power rule integration.

Importance of Practice Problems and Mock Exams

Consistent practice is key to mastering any subject, especially when preparing for assessments. Engaging in regular practice problems and taking mock tests helps reinforce concepts, identify areas that need improvement, and build confidence. It not only allows you to familiarize yourself with the types of questions that may appear, but also helps you develop the skills to approach problems efficiently under time constraints.

Mock exams, in particular, simulate the pressure and environment of the real test, making them an invaluable tool for preparation. By timing yourself and working through a full set of problems, you gain insight into your pacing and identify which topics require further review. The process of self-testing also enhances long-term retention and can make the material more accessible during the actual assessment.

Key Benefits of Practice Problems

Working through practice problems regularly offers several benefits that improve both your understanding and test-taking performance:

Reinforces Learning: Frequent problem-solving helps solidify key concepts and methods.
Builds Test-Taking Speed: Solving problems under time pressure improves your ability to manage time during the test.
Identifies Weak Areas: Practice helps pinpoint topics that need more focus and clarification.
Boosts Confidence: The more problems you solve, the more confident you become in your ability to tackle different questions.

How Mock Tests Prepare You

Taking full-length mock tests helps prepare for the overall test experience. These practice sessions offer a more comprehensive look at how you perform under real conditions:

Mock Test Benefits	Why It’s Important
Simulate Test Conditions	Helps you manage time and stress effectively during the actual assessment.
Full Practice	Prepares you for the structure and flow of the actual test, providing experience with all question types.
Review Mistakes	Provides an opportunity to review errors and solidify understanding in weaker areas.

Time Management Strategies for the Test

Effective time management is essential when preparing for and taking any assessment. The ability to allocate your time wisely during a test can greatly influence your performance. By planning ahead and staying organized, you can ensure that you address each question thoughtfully while avoiding unnecessary stress. Developing strategies for managing time efficiently will not only help you complete the test on time but also allow you to focus on each section without feeling rushed.

During the assessment, it’s crucial to maintain a steady pace. Overthinking or spending too much time on any one problem can lead to unfinished sections and missed opportunities to score points. By practicing time allocation techniques, you can improve your overall efficiency and approach the test with a clear and focused mindset.

Pre-Test Time Management Tips

Practice Timed Problems: Simulate test conditions by solving practice questions within a time limit to build familiarity with pacing.
Prioritize Difficult Questions: Tackle challenging problems early to ensure you don’t get stuck later when time is running out.
Know Your Strongest Areas: Identify which sections you can complete quickly and accurately, allowing you to save more time for difficult questions.

During the Test: Managing Your Time

Allocate Time for Each Section: Break down the test into sections and assign a specific amount of time to each, ensuring that you don’t spend too long on any one part.
Skip and Return: If you get stuck on a problem, move on to the next one and come back to it later if you have time remaining.
Monitor Your Progress: Keep an eye on the clock throughout the test to ensure you’re staying on track and adjust your pace as needed.

Using Mathematical Formulas Effectively

Mastering and applying key mathematical formulas is crucial for solving problems efficiently. Knowing when and how to use specific equations can significantly improve your problem-solving skills and save time during an assessment. Rather than memorizing formulas in isolation, it is essential to understand their derivation, applications, and connections to broader concepts. This deep understanding allows you to approach problems strategically and choose the most effective methods for solving them.

It is equally important to be aware of common pitfalls and strategies to avoid errors when applying these formulas. Ensuring you select the right formula for each problem is vital, as using an inappropriate equation can lead to confusion and wasted time. Regular practice with various types of problems will help reinforce your ability to recognize which formulas to use in different situations.

Review Key Formulas: Focus on the most commonly used equations, such as those related to differentiation, integration, and limits, ensuring you know how and when to apply them.
Understand the Context: Before applying a formula, carefully read the problem to ensure you are using the right one for the given situation.
Practice Formula Derivations: Understanding how formulas are derived will help reinforce their meaning and correct application in various contexts.
Double-Check Units: Always make sure the units in the formula match those in the problem to avoid errors in your solution.

What to Do on Assessment Day

On the day of the test, it’s essential to approach the situation with a clear mind and a positive attitude. Preparing yourself both mentally and physically is key to performing well. This means ensuring you have all necessary materials, arriving at the test location on time, and being ready to focus fully on the task at hand. The way you manage your time and approach the test will directly impact your performance.

Before the test begins, take a moment to relax and clear your thoughts. Do not rush into the questions immediately; instead, take a few deep breaths and give yourself time to adjust. This can help reduce anxiety and set the tone for a calm, focused approach to the assessment.

Arrive Early: Make sure you reach the location with enough time to get settled and avoid any last-minute stress.
Bring All Required Materials: Ensure you have all essential items, such as writing tools, a calculator (if allowed), and any necessary identification or documents.
Stay Calm: Take a few moments to breathe deeply and relax before starting. Staying calm will help you think more clearly throughout the test.
Read Instructions Carefully: Pay attention to any specific instructions or guidelines provided at the beginning of the test.
Manage Your Time: Be mindful of how much time you have for each section and avoid spending too long on any single problem.

How to Stay Calm and Focused

Maintaining composure and concentration during a high-pressure situation can be challenging, but it is crucial for achieving success. By developing strategies to manage stress and stay engaged with the task, you can perform to the best of your ability. Staying calm helps you think clearly, make fewer mistakes, and tackle problems effectively.

One effective approach is to focus on deep, controlled breathing. This simple technique can help lower anxiety levels and bring your mind back to the present moment. When you feel your thoughts racing, take a moment to breathe in slowly through your nose, hold briefly, and exhale through your mouth. This can help to slow your heart rate and clear your mind.

Practice Mindfulness: Stay present by focusing on one problem at a time, and avoid thinking too far ahead or dwelling on past questions.
Take Short Breaks: If allowed, take a few moments to stretch or close your eyes briefly. This can help reset your mind and relieve tension.
Stay Positive: Remind yourself that you are prepared. Positive self-talk can help reduce anxiety and increase confidence.
Trust Your Preparation: Focus on the work you’ve done leading up to the assessment. Trust in your ability to solve the problems based on your prior practice and knowledge.
Keep a Steady Pace: Don’t rush. Maintain a consistent pace throughout the assessment to avoid unnecessary stress or mistakes.