
Mastering fundamental principles in advanced mathematics requires consistent practice and a deep understanding of core concepts. The ability to solve a variety of problems not only strengthens skills but also builds confidence. This section provides essential practice exercises to test and refine your knowledge in various mathematical topics.
By engaging with diverse problem types, learners can improve their problem-solving techniques and tackle more complex scenarios. Each problem is carefully crafted to challenge your grasp of critical concepts while offering detailed solutions to guide your learning process. The goal is to enhance both speed and accuracy in tackling complex mathematical challenges.
Testing your abilities through hands-on exercises allows for better retention and comprehension. As you work through these examples, you’ll gain a clearer understanding of how to apply mathematical rules and techniques effectively in real-world situations. Embrace each challenge as an opportunity to grow and strengthen your foundational skills.
Calculus Multiple Choice Questions with Answers
This section presents a variety of exercises designed to assess your understanding of key mathematical principles. By engaging in problem-solving, you’ll reinforce your grasp of critical concepts and improve your analytical skills. Each example provides a clear solution that guides you through the necessary steps, helping to solidify your knowledge.
Basic Derivative Problems
These exercises focus on finding derivatives of basic functions. They help sharpen your ability to apply fundamental rules and techniques.
- Find the derivative of f(x) = 3x^2 + 5x – 7.
- Determine the rate of change of g(x) = x^3 – 4x + 2.
- Evaluate the derivative of h(x) = sin(x) + cos(x).
Integral and Limit Applications
This section tests your skills in integrating functions and working with limits. These are essential tools for solving more advanced problems.
- Calculate the integral of f(x) = 4x^3 – 2x + 1.
- Find the limit of f(x) = (x^2 – 1)/(x – 1) as x approaches 1.
- Evaluate the area under the curve of y = x^2 from 0 to 3.
By practicing these problems, you’ll develop a deeper understanding of mathematical methods and be able to apply them confidently to more complex challenges.
Mastering Derivatives Through Practice
Developing a solid understanding of how to calculate rates of change is essential for progressing in advanced mathematics. By practicing various types of problems, you can refine your technique, learn to recognize patterns, and apply differentiation rules effectively in diverse scenarios. Repeated exercises will improve both your speed and precision when solving such problems.
Here are some sample problems to help you get started:
| Function | Problem | Solution |
|---|---|---|
| f(x) = 5x^3 + 4x^2 | Find the derivative of f(x) | f'(x) = 15x^2 + 8x |
| g(x) = e^x + 3x | Determine the derivative of g(x) | g'(x) = e^x + 3 |
| h(x) = ln(x) – x^2 | Calculate the derivative of h(x) | h'(x) = 1/x – 2x |
By working through a range of problems like these, you will begin to internalize the process of differentiation and build confidence in solving related problems. Over time, your ability to quickly and accurately calculate derivatives will improve significantly, enabling you to tackle more complex topics.
Understanding Integrals with Examples
Grasping the concept of finding areas under curves and solving problems involving accumulation is crucial for advancing in higher-level mathematics. Through practice, you can learn to apply integration techniques to various types of functions, building a deeper understanding of their applications and relevance.
Basic Integration Problems
This section provides examples that will help you understand the fundamentals of integration. By solving these problems, you can start to see how integral functions work and how they are related to areas and accumulations.
- Integrate f(x) = 2x + 3.
- Find the integral of g(x) = x^2 – 4x + 5.
- Calculate the integral of h(x) = 6x^3.
Advanced Integration Examples
Once you’re comfortable with the basics, move on to more challenging problems that involve more complex functions and require advanced techniques for solving.
- Evaluate the integral of f(x) = 3e^x.
- Find the integral of g(x) = sin(x) + cos(x).
- Calculate the integral of h(x) = 1/x.
As you practice these examples, you’ll gain a better understanding of how to approach different types of integral problems and how these concepts are used in real-world applications. Regular practice is key to mastering this skill.
Application of Limits in Calculus
Understanding how functions behave as they approach certain values is fundamental in various areas of mathematics. The concept of examining the behavior of a function as it approaches a specific point helps solve complex problems in fields like physics, engineering, and economics. This technique enables the analysis of real-world systems where values are continuously changing.
Limits in Real-World Problems
Limits are applied to model various natural phenomena. For example, they can be used to determine the instantaneous rate of change in motion or the behavior of a system as it reaches equilibrium.
- Finding the instantaneous velocity of an object moving along a path.
- Determining the population growth rate as time approaches infinity.
- Analyzing the concentration of a substance as it approaches a specific value in a chemical reaction.
Key Techniques for Evaluating Limits
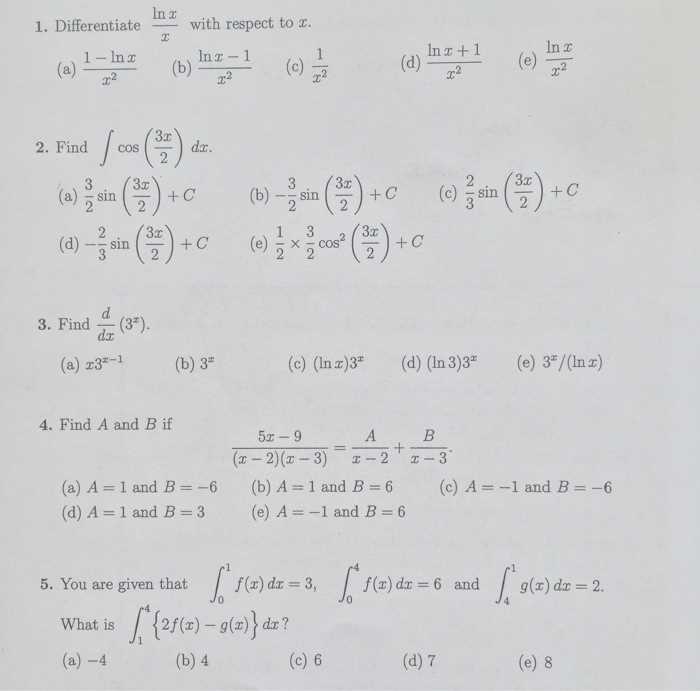
There are different methods to calculate the limit of a function, and learning these techniques will allow you to solve a wide range of problems. Here are some common approaches:
- Direct substitution, where you substitute the point into the function.
- Factorization, useful when direct substitution results in an indeterminate form.
- L’Hopital’s Rule, a powerful method for dealing with indeterminate limits like 0/0 or ∞/∞.
By applying these techniques, you can confidently solve problems and deepen your understanding of the continuous behavior of functions. Mastery of limits is a crucial step in tackling more complex topics in mathematics and related fields.
Improving Problem-Solving Speed
Enhancing the ability to solve problems quickly is essential for mastering mathematical concepts. By practicing regularly and using efficient strategies, you can improve both your speed and accuracy when tackling complex tasks. Developing these skills allows you to work through exercises more effectively and perform better under time constraints.
Techniques for Faster Problem Solving
There are several strategies that can help speed up the process of solving problems. Below are some tips for becoming more efficient:
- Familiarize yourself with common formulas: Knowing key equations and their applications saves time during calculations.
- Break down complex problems: Simplifying the problem into smaller, more manageable parts can make it easier to solve.
- Practice mental math: Strengthening mental calculation skills can reduce dependence on a calculator and speed up your solutions.
- Use shortcuts: Learning techniques like factoring or substitution can help solve problems in fewer steps.
Regular Practice and Time Management
Speed comes with consistent practice. The more problems you solve, the quicker you’ll recognize patterns and apply techniques. Here are a few ways to improve your efficiency:
- Set a timer while practicing to simulate exam conditions and help improve your pace.
- Work on a variety of problem types to build versatility in your approach.
- Review and learn from mistakes to avoid repeating errors in the future.
By incorporating these strategies and focusing on continuous improvement, you can boost your ability to solve problems faster and with greater precision, ultimately achieving better results in mathematical exercises.
Common Mistakes in Calculus Tests
When tackling advanced mathematical problems, students often make certain errors that can hinder their performance. These mistakes are usually due to misunderstandings of fundamental concepts, improper application of techniques, or simple calculation errors. Identifying and addressing these issues can significantly improve your results and boost your confidence during exams.
Frequent Errors in Problem Solving
Many students fall into the trap of overlooking key steps or misapplying rules. Below are some common mistakes to watch out for:
- Forgetting to apply the chain rule: When differentiating composite functions, it’s easy to forget to apply the chain rule, which leads to incorrect results.
- Misapplying integration constants: Often, students forget to add the constant of integration after performing indefinite integration.
- Incorrect limits of integration: Not properly setting up the bounds in definite integrals can result in wrong calculations and answers.
- Failing to simplify expressions: Some problems require simplifying expressions before applying a formula, and skipping this step can lead to errors.
How to Avoid These Mistakes
Recognizing these common pitfalls is the first step in overcoming them. To improve your accuracy:
- Double-check your work: Always go back and verify your calculations before finalizing your answer.
- Practice regularly: The more problems you solve, the better you’ll understand the techniques and reduce the chance of making errors.
- Review foundational concepts: Strong knowledge of basic principles ensures you can apply advanced techniques correctly.
By being mindful of these common errors and practicing regularly, you can improve your performance and avoid mistakes that often lead to incorrect solutions in tests.
Exploring Optimization Problems in Calculus
Optimization problems are essential in many fields, where the goal is to find the maximum or minimum value of a function within a given context. These problems often arise in real-world scenarios such as maximizing profit, minimizing cost, or finding the most efficient solution to a problem. Understanding how to approach these types of tasks involves using critical points and analyzing the behavior of a function.
Understanding the Process
The process of solving optimization problems typically involves a few key steps:
- Define the objective function you want to maximize or minimize.
- Find the derivative of the function to determine critical points.
- Use the second derivative test or other methods to confirm whether the critical points correspond to maximum or minimum values.
- Consider the boundaries of the domain, as the maximum or minimum might occur at the endpoints.
Real-World Examples
Optimization problems are often applied to solve practical challenges. Here are a few examples:
- Maximizing the area of a rectangular fence with a fixed perimeter.
- Minimizing the cost of materials for constructing a container with a fixed volume.
- Maximizing profit based on cost and revenue functions in a business scenario.
By applying these techniques to various situations, you can efficiently solve optimization problems and find the optimal solutions needed in real-world contexts.
Techniques for Solving Rate Problems
Rate problems are a common type of word problem that involve the relationship between quantities changing over time. Whether you’re dealing with speed, flow, or any other type of rate, these problems often require applying fundamental principles and finding relationships between different variables. Mastering the techniques to solve rate problems is crucial for tackling a variety of scenarios in both academic and real-world contexts.
Key Steps in Solving Rate Problems
To solve these problems efficiently, follow these essential steps:
- Identify the given values: Start by identifying the rates and other quantities provided in the problem, such as distance, time, or volume.
- Set up a formula: Most rate problems involve a basic formula, such as distance = rate × time, or work = rate × time.
- Express the unknown: Determine which variable you need to solve for, and then rearrange the formula to isolate that variable.
- Substitute known values: Substitute the known values into the equation and solve for the unknown.
Common Types of Rate Problems
Here are some examples of common rate problems you might encounter:
- Travel and Speed: Finding the time it takes to travel a certain distance at a specific speed.
- Work Rate: Solving problems where two or more individuals or machines are working together at different rates to complete a task.
- Flow Rate: Calculating the flow of a substance (such as water or air) through a pipe or channel at a given rate.
By practicing these techniques and understanding the underlying principles, you can effectively solve a wide range of rate problems in different settings.
Using the Fundamental Theorem of Calculus
The Fundamental Theorem provides a powerful connection between two key concepts: differentiation and integration. This theorem simplifies the process of finding definite integrals by allowing the use of antiderivatives. By applying this principle, one can evaluate the area under a curve or solve various problems that involve accumulated quantities. Understanding how to effectively use this theorem is crucial for solving complex mathematical problems efficiently.
Understanding the Core Concepts
The theorem consists of two main parts, each of which plays a critical role in solving integrals:
- Part 1: This part shows that if a function is continuous, its integral can be evaluated using an antiderivative of the function.
- Part 2: It asserts that the derivative of an integral function is the original integrand itself, providing an easy way to compute the rate of change of an accumulated quantity.
Applying the Fundamental Theorem
Here’s how you can use this concept in practical problems:
- Identify the integrand: First, determine the function you need to integrate.
- Find an antiderivative: Use known techniques or formulas to find the antiderivative of the given function.
- Evaluate the limits: Plug in the upper and lower limits of the integral into the antiderivative and subtract the results.
By applying these steps, you can efficiently solve definite integrals and relate accumulated quantities to rates of change, making this principle a cornerstone of advanced mathematical applications.
How to Tackle Chain Rule Questions
The chain rule is a powerful tool used to differentiate composite functions. When faced with problems that involve functions within functions, this technique allows you to break down complex derivatives into simpler parts. By understanding the structure of the function and applying the chain rule step by step, you can solve these problems efficiently and correctly.
To solve a problem using the chain rule, follow these key steps:
- Identify the outer and inner functions: Look for the function that is inside another function. The inner function is typically the one that is being composed, while the outer function is the one that operates on it.
- Differentiate the outer function: Take the derivative of the outer function as if the inner function were a single variable.
- Differentiate the inner function: Next, differentiate the inner function in its original form.
- Multiply the results: Finally, multiply the derivative of the outer function by the derivative of the inner function.
By practicing these steps, you can handle complex derivative problems that involve nested functions and improve your ability to differentiate efficiently. The chain rule simplifies what would otherwise be a difficult process, allowing you to solve a variety of problems with ease.
Strategies for Definite and Indefinite Integrals
Integrating functions is an essential process in many mathematical problems. Whether you’re dealing with a definite integral, which calculates the accumulated quantity over a specific interval, or an indefinite integral, which finds the general antiderivative, understanding the techniques to approach both types is crucial for solving complex problems. Each type requires distinct strategies, but both share foundational principles that can be applied effectively with practice.
Approaching Indefinite Integrals

Indefinite integrals focus on finding a general antiderivative for a given function. Here’s how to approach them:
- Identify the form: Recognize the structure of the function to determine which basic integration rule to apply, such as the power rule, substitution, or integration by parts.
- Find the antiderivative: Apply the appropriate integration technique to find the general antiderivative.
- Include the constant: Always remember to add the constant of integration (C), which represents the family of all antiderivatives.
Handling Definite Integrals
Definite integrals involve calculating the net area under a curve over a specific interval. Here’s how to solve them:
- Set the limits: Identify the upper and lower bounds of the integral, which define the region of interest.
- Evaluate the antiderivative: First, find the antiderivative of the function (just as you would for an indefinite integral).
- Substitute the limits: Plug in the upper and lower limits into the antiderivative and subtract the values to find the total area.
Common Techniques and Tips
| Technique | When to Use |
|---|---|
| Substitution | Use when the integrand contains a composite function that can be simplified by changing variables. |
| Integration by Parts | Apply when the integrand is a product of two functions that are easy to differentiate and integrate separately. |
| Partial Fractions | Use when the integrand is a rational function that can be decomposed into simpler fractions. |
By mastering these strategies, you can confidently solve both indefinite and definite integrals, whether you’re dealing with straightforward functions or more complex cases.
Enhancing Your Understanding of Sequences
Sequences are an essential concept in mathematics, involving ordered lists of numbers that follow a specific pattern or rule. Understanding the behavior of these sequences and how to analyze them is crucial for solving problems that deal with series, limits, and various other mathematical concepts. Developing a strong grasp of sequences not only strengthens your overall mathematical foundation but also enhances problem-solving skills for more complex scenarios.
To improve your understanding of sequences, it’s important to recognize key properties such as convergence, divergence, and the general term that defines each sequence. Identifying these properties allows you to predict the behavior of the sequence as it progresses, which is useful for determining limits or sums. Additionally, learning how to manipulate sequences algebraically helps solve problems that involve recursive formulas or other sequence-based operations.
Here are a few strategies to enhance your understanding:
- Practice identifying patterns: Look for arithmetic or geometric progressions and familiarize yourself with their respective formulas.
- Understand the concept of limits: Knowing how sequences behave as they approach infinity is key to analyzing their convergence or divergence.
- Work with recursive sequences: Recursive sequences are defined by a formula that references previous terms, so practice solving these types to see how they unfold.
By regularly working through problems involving sequences and applying these strategies, you can build a deeper understanding of this crucial mathematical concept.
Key Tips for Success in Exams
Achieving success in exams requires more than just memorizing formulas and definitions. It involves understanding the concepts deeply, applying problem-solving strategies, and managing your time effectively. By adopting the right approach, you can tackle even the most challenging problems with confidence and clarity.
Effective Study Techniques
To maximize your performance, start by focusing on understanding the core principles rather than rote memorization. Use the following strategies to build a solid foundation:
- Master the Basics: Ensure you have a strong understanding of fundamental concepts before tackling more complex topics. Reviewing foundational material will make advanced problems easier to solve.
- Practice Regularly: Consistent practice helps reinforce concepts and improves problem-solving speed. Work through a variety of problems, from simple to advanced, to enhance your skills.
- Use Study Groups: Collaborative learning can help you identify gaps in your understanding and provide different perspectives on how to solve problems.
Time Management Strategies
During the exam, managing your time is crucial for completing all the tasks efficiently. Use these tips to stay on track:
- Prioritize Easy Problems: Start with questions that you find easiest, as this will help build confidence and ensure you gain quick points.
- Allocate Time Wisely: Keep track of time and set limits for each section to avoid spending too long on any one problem.
- Review Your Work: If time allows, always review your solutions to check for errors and ensure accuracy before submitting.
By following these strategies, you’ll be well-equipped to succeed in your exams and tackle even the most difficult problems with ease.
Choosing Between L’Hopital’s Rule and Limits
When dealing with indeterminate forms, two essential methods often come into play: L’Hopital’s Rule and direct evaluation using limits. Both techniques are valuable tools in solving complex problems, but knowing when to apply each can significantly simplify the process and yield accurate results.
Understanding the nature of the problem is key to deciding which method to use. Sometimes, straightforward limit evaluation is sufficient, while in other cases, L’Hopital’s Rule provides a quicker and more effective approach.
When to Use L’Hopital’s Rule
L’Hopital’s Rule is particularly useful when you encounter indeterminate forms like 0/0 or ∞/∞. It allows you to differentiate the numerator and denominator and then re-evaluate the limit. Consider using L’Hopital’s Rule in the following scenarios:
- Indeterminate Forms: When you get 0/0 or ∞/∞, L’Hopital’s Rule is often the most efficient method.
- Repeated Indeterminate Forms: If applying L’Hopital’s Rule results in another indeterminate form, you can apply the rule multiple times until you get a solvable expression.
- Complex Functions: For functions involving trigonometric, exponential, or logarithmic terms, L’Hopital’s Rule can often simplify the calculation by reducing the complexity.
When to Use Direct Limit Evaluation
In many cases, limits can be evaluated directly without the need for differentiation. Direct evaluation is often more straightforward and should be your first approach if the problem doesn’t involve indeterminate forms. Use this method in these situations:
- Simple Forms: If the limit can be directly calculated by substitution without encountering an indeterminate form, it’s best to go with direct evaluation.
- Continuous Functions: For continuous functions where the limit can be easily found by plugging in the value, direct evaluation is the simplest solution.
- Piecewise Functions: When dealing with piecewise functions, check for continuity at the given point and evaluate the limit directly based on the function’s definition.
By understanding when to apply L’Hopital’s Rule versus direct limit evaluation, you can tackle a wider range of problems with efficiency and precision.
Breaking Down Advanced Calculus Topics

As you advance in your mathematical studies, certain topics become more intricate and require a deeper understanding. These concepts often involve higher-level techniques and abstract reasoning. Breaking down these complex ideas step by step can help make them more approachable and manageable.
In this section, we will explore some of the most challenging areas and discuss how to simplify them. By understanding the underlying principles and applying systematic approaches, you’ll be able to tackle these advanced topics with confidence.
Techniques in Multivariable Functions
Working with functions of multiple variables can be overwhelming, but understanding key concepts like partial derivatives and multiple integrals is crucial. Here’s how to approach these:
- Partial Derivatives: Focus on how each variable affects the function independently, and use this to find the rate of change in a specific direction.
- Double and Triple Integrals: These integrals extend the concept of integration to higher dimensions. Practice setting up limits based on the problem’s geometry and applying the appropriate method.
Series and Sequences: Convergence and Divergence
Series and sequences are foundational topics in higher mathematics, requiring an understanding of convergence and divergence. Here’s how to break them down:
- Convergence Tests: Learn how to apply tests such as the ratio test, root test, and comparison test to determine if a series converges or diverges.
- Power Series: Explore how power series represent functions and practice finding their radius and interval of convergence.
By approaching these advanced topics methodically, you can master complex concepts and apply them effectively in solving problems.
Understanding Series Convergence and Divergence
When dealing with infinite sums, understanding whether the series converges or diverges is a fundamental concept. Convergence indicates that the sum approaches a specific value, while divergence means that the sum does not approach any finite value, either growing without bound or oscillating. Mastering these concepts is essential for solving problems involving series in mathematical analysis.
In this section, we will examine how to determine the behavior of a series using various tests, and how to identify whether it converges to a finite value or diverges. These principles are pivotal for analyzing functions and solving problems in higher-level mathematics.
Common Tests for Convergence and Divergence
Several techniques exist to help assess the convergence or divergence of a series. These methods focus on comparing the series with known convergent or divergent series or evaluating the limit of its terms.
| Test | Description | When to Use |
|---|---|---|
| Ratio Test | Uses the ratio of consecutive terms to determine convergence. If the limit of the ratio is less than 1, the series converges; if greater than 1, it diverges. | Useful for series with factorials or exponential terms. |
| Root Test | Relates the nth root of the terms in the series. If the limit of the nth root is less than 1, the series converges. | Effective for series involving powers or nth roots. |
| Comparison Test | Compares the series with a known convergent or divergent series. If the series behaves similarly to a known series, its behavior can be determined. | Best used when a comparison with a simpler series is possible. |
| Integral Test | Relates the series to an improper integral. If the integral converges, so does the series. | Suitable for series that resemble integrals of continuous functions. |
Practical Examples of Convergence and Divergence
Let’s apply the tests to a few examples to see how these methods work in practice. For instance, consider the series:
- For the series Σ 1/n^2, the comparison test can be used with a known convergent p-series, leading to the conclusion that it converges.
- On the other hand, the series Σ 1/n is a harmonic series, which diverges by the integral test.
By systematically applying these tests, you’ll be able to analyze the behavior of a series and make informed conclusions about its convergence or divergence.