Core Connections Algebra 2 Answers Guide

Understanding the fundamentals of higher-level mathematics is essential for students aiming to succeed in their studies. This section provides a comprehensive guide to tackling complex problems and offers a range of methods for simplifying intricate concepts. Whether you’re reviewing key principles or seeking clarification on difficult topics, this resource will help enhance your problem-solving skills.

Step-by-step solutions and detailed explanations are designed to break down each challenge into manageable parts. From equations to graphing, the focus is on building a strong foundation and reinforcing essential strategies for approaching advanced math. With consistent practice, these techniques will help you develop a deeper understanding and improve your ability to handle various mathematical situations with confidence.

By following the approaches outlined here, you can strengthen your knowledge and boost your performance in tackling more advanced coursework. With clear instructions and carefully selected problems, mastering even the most complex areas of math becomes an achievable goal.

Core Connections Algebra 2 Answers Overview

Understanding advanced mathematical principles is crucial for students progressing through their coursework. This section offers an in-depth look at the key strategies and resources available to tackle the more complex topics found in higher-level mathematics. By breaking down each concept and providing clear explanations, this guide helps students not only grasp the material but also apply the knowledge effectively.

Key Topics Covered

Solving linear and quadratic equations
Understanding functions and their properties
Graphing and interpreting mathematical models
Working with polynomials and rational expressions
Systems of equations and inequalities
Analyzing real-world scenarios with mathematical reasoning

How This Resource Helps

Each section focuses on a specific area, providing step-by-step instructions for solving problems, tips for identifying common errors, and practice problems designed to reinforce learning. This method allows students to build a solid understanding of each concept, which in turn prepares them for more advanced topics.

By working through the solutions and examples provided, learners will develop critical thinking skills and improve their ability to approach math problems with confidence. Whether you’re preparing for exams or simply looking to strengthen your understanding, these resources will support your learning journey and enhance your problem-solving abilities.

Understanding Key Algebra 2 Concepts

Mastering the essential concepts of advanced mathematics requires a clear understanding of fundamental principles that form the foundation for more complex topics. This section delves into the core elements that every student must grasp in order to succeed. These concepts range from basic operations to intricate problem-solving strategies that involve multiple steps.

The ability to recognize and apply these ideas is key to progressing through higher-level math courses. By understanding functions, equations, and their various properties, students can approach a wide variety of problems with the right techniques and tools. This section highlights the most important topics, providing a clear roadmap for effective learning and application.

Step-by-Step Algebra 2 Solution Methods

Breaking down complex mathematical problems into manageable steps is essential for achieving clarity and accuracy. This section focuses on the process of solving intricate problems systematically, ensuring that each part of the equation is tackled in a logical sequence. By following these methods, students can efficiently address a wide range of challenges and improve their problem-solving skills.

Steps for Solving Equations

Identify the type of equation and the methods required to solve it.
Isolate the variable on one side of the equation.
Perform inverse operations to simplify both sides.
Check the solution by substituting it back into the original equation.

Key Techniques for Problem-Solving

Factoring expressions to simplify equations.
Graphing to visualize relationships between variables.
Using substitution or elimination to solve systems of equations.
Applying the quadratic formula for complex solutions.

By consistently practicing these methods, students will develop a stronger understanding of the problem-solving process and be able to apply the techniques to more advanced topics with confidence.

Common Mistakes in Algebra 2 Problems

Even experienced learners can make errors when working through complex mathematical problems. Understanding these common mistakes and learning how to avoid them is essential for improving accuracy and confidence. In this section, we’ll highlight the frequent missteps that students encounter and provide guidance on how to prevent them.

One of the most common issues is overlooking important details in the problem, such as missing parentheses or misinterpreting signs. These simple errors can lead to incorrect results, especially when solving multi-step equations. Additionally, improper handling of fractions or exponents can also cause confusion. Identifying these pitfalls early and practicing careful attention to detail can significantly reduce the likelihood of mistakes.

Forgetting to apply the distributive property correctly.
Misapplying the order of operations (PEMDAS).
Incorrectly simplifying complex fractions or expressions.
Overlooking negative signs when solving equations.
Using the wrong formula for specific problem types.

By being aware of these common mistakes and practicing mindful techniques, students can improve their problem-solving skills and ensure more accurate results in their work.

Tips for Solving Algebra 2 Equations

Solving complex equations requires a strategic approach to ensure accuracy and efficiency. This section provides essential tips that help break down difficult problems and guide you through the solution process step by step. By applying these techniques, you can build a stronger foundation in mathematical problem-solving and reduce the chance of errors.

Key Strategies for Success

Always start by identifying the type of equation you are dealing with. This will help you determine the best method for solving it.
Simplify both sides of the equation as much as possible before isolating the variable.
Use inverse operations to move terms across the equation, remembering to flip the signs where necessary.
Double-check each step to ensure no simple mistakes, such as arithmetic errors or sign mismanagement.

Additional Tips for Efficiency

If the equation involves fractions, multiply both sides by the least common denominator (LCD) to eliminate fractions.
For equations with exponents, remember to follow the power rules carefully.
In complex problems, break them down into smaller, more manageable parts to avoid becoming overwhelmed.
Always check your final solution by substituting it back into the original equation to verify that it satisfies the conditions.

By applying these tips and practicing regularly, you’ll find that solving advanced equations becomes a more structured and less daunting task, boosting both your confidence and performance.

How to Use Core Connections Effectively

To succeed in advanced math courses, it’s essential to leverage available resources effectively. Understanding how to make the most of problem-solving guides and learning tools will enable students to navigate complex concepts with confidence. This section offers practical strategies for utilizing study materials in a way that enhances understanding and retention of key topics.

Organizing Your Study Approach

Begin by thoroughly reviewing the provided examples and solutions. These will help you understand the thought process behind each problem.
Take notes while studying, summarizing key techniques and steps for solving different types of equations and expressions.
Work through practice problems regularly to reinforce your understanding and improve problem-solving speed.
When you encounter difficulties, break the problem down into smaller, more manageable parts, referring back to the examples for guidance.

Maximizing Your Practice Sessions

Use a variety of problem sets to expose yourself to different scenarios and question types.
Focus on mastering one concept at a time before moving on to the next, ensuring a strong grasp of each topic.
Work with peers or tutors to discuss challenging problems and share approaches for tackling them effectively.

By following these strategies and staying consistent with your practice, you’ll gain a deeper understanding of complex concepts and improve your overall performance in advanced math coursework.

Algebra 2 Answer Key Insights

Understanding the solutions to mathematical problems is as important as solving them. This section offers insights into how answer keys can provide valuable guidance when approaching challenging equations and expressions. By analyzing the steps presented in the solutions, students can uncover the reasoning behind each step and improve their problem-solving skills for future tasks.

Breaking Down the Solution Process

Each answer key typically follows a structured process, starting from identifying the correct method to applying the necessary operations step-by-step. Carefully studying these steps not only clarifies the method used but also reinforces key concepts. This allows students to internalize the solution approach and apply it to similar problems in their studies.

Key Takeaways from Solution Guides

Concept	Explanation	Application
Equation Simplification	Breaking down complex expressions into simpler components.	Helps in recognizing common patterns in problems.
Inverse Operations	Using the opposite operation to isolate variables.	Vital for solving equations accurately and efficiently.
Graphical Interpretation	Understanding solutions through visual representation.	Essential for analyzing relationships between variables.
Factoring	Rewriting expressions as a product of simpler terms.	Common method for solving quadratics and polynomials.

By referring to these solution guides, students can identify key techniques that will help them solve similar problems in the future. These insights foster a deeper understanding of mathematical concepts and contribute to the development of stronger analytical skills.

Practice Problems and Solutions for Mastery

To truly master advanced mathematical concepts, consistent practice is essential. Engaging with a variety of problems helps reinforce key principles and ensures a deep understanding of the material. In this section, we provide a selection of practice problems along with their solutions to guide you through the process of mastering different techniques.

By working through these problems step-by-step, students can solidify their understanding of key concepts, such as solving equations, graphing functions, and working with polynomials. Each solution is broken down to highlight the necessary steps, helping to identify common challenges and build problem-solving confidence.

Practice Problems

Solve the equation: 2x + 5 = 15
Factor the expression: x² – 9
Graph the function: y = 2x – 4
Simplify the expression: (3x + 4)² – (x – 2)²
Find the roots of the quadratic equation: x² + 5x + 6 = 0

Solutions Breakdown

Equation 1: 2x + 5 = 15
- Subtract 5 from both sides: 2x = 10
- Divide by 2: x = 5
Equation 2: x² – 9
- Recognize as a difference of squares: (x – 3)(x + 3)
Equation 3: y = 2x – 4
- Plot points using x-values and solve for y.
- Draw a straight line through the points.
Equation 4: (3x + 4)² – (x – 2)²
- Apply the difference of squares formula: (a² – b²) = (a – b)(a + b).
- Factor and simplify the resulting terms.
Equation 5: x² + 5x + 6 = 0
- Factor the quadratic expression: (x + 2)(x + 3) = 0
- Set each factor equal to 0: x + 2 = 0 or x + 3 = 0
- Solve for x: x = -2 or x = -3

By regularly practicing problems like these, students can improve their proficiency and confidence in solving complex problems. The key to mastery lies in repeated exposure and applying the learned techniques to a wide range of scenarios.

Mastering Functions in Algebra 2

Understanding functions is crucial to succeeding in advanced mathematics. Functions provide a way to model relationships between variables and solve real-world problems. Mastery of this concept allows students to analyze and interpret various mathematical scenarios with ease. In this section, we will explore key strategies for mastering functions, including how to work with different types of functions, interpret graphs, and apply functions to problem-solving tasks.

Key Concepts in Functions

Domain and Range: Recognizing the set of possible input (domain) and output (range) values is essential in understanding the behavior of a function.
Function Notation: Familiarizing yourself with the notation f(x) and understanding how to use it to represent and manipulate functions is critical for simplifying problems.
Types of Functions: Learn to identify and work with linear, quadratic, exponential, and other common function types, each of which has unique properties and applications.
Inverse Functions: Understanding how to find the inverse of a function is key when solving equations that involve function relationships.

Strategies for Mastering Functions

Graphing: Practice graphing different types of functions to visualize their behavior and understand the impact of changes in the equation on the graph.
Using Tables: When solving problems, use tables to organize inputs and outputs to identify patterns or trends in the function.
Solve Function Equations: Solve equations involving functions by isolating the variable, applying inverse operations, and using known function properties.
Practice Word Problems: Apply your knowledge of functions to real-world situations by solving word problems, which will help develop your ability to translate verbal descriptions into mathematical functions.

By following these strategies and continuously practicing different types of function problems, you’ll build a strong foundation and gain confidence in working with functions in advanced math courses.

Interpreting Graphs in Algebra 2

Graphs provide a visual representation of mathematical relationships, making them essential for understanding complex concepts. By interpreting graphs, students can better analyze functions, identify key features, and solve equations more effectively. This section will guide you through the process of reading and interpreting various types of graphs, with a focus on extracting meaningful information from them to solve problems and make predictions.

Key Features of Graphs

When interpreting graphs, it’s important to identify the following key features:

Intercepts: Points where the graph crosses the x-axis (x-intercepts) and the y-axis (y-intercepts). These points are often solutions to equations.
Slopes: The steepness or incline of a line, indicating the rate of change. This is particularly important in linear functions.
Maximum and Minimum Points: The highest or lowest points on the graph, often indicating turning points for quadratic or cubic functions.
Asymptotes: Lines that the graph approaches but never touches, commonly seen in rational functions or exponential decay models.

Steps for Interpreting Graphs

Follow these steps to effectively interpret graphs and extract the necessary information:

Examine the axes: Always begin by identifying the scale and labels of the x-axis and y-axis. This ensures that you understand the units and range represented in the graph.
Identify the type of graph: Determine whether the graph represents a linear, quadratic, exponential, or another function type. This helps guide your analysis of the graph’s behavior.
Look for key features: Identify intercepts, slopes, turning points, and any asymptotes or other relevant characteristics of the graph.
Analyze trends: Pay attention to the overall behavior of the graph, including whether it increases or decreases and how the graph behaves at extreme values of x.

Graph Interpretation Example

Consider the following graph of a quadratic function:

x-value	y-value
-2	4
0	0
2	4

This table represents a quadratic function with roots at x = 0 and a vertex at (0, 0). The function opens upward, and the y-values increase as the x-values move away from zero in either direction. By analyzing this graph, we can conclude that the function has a minimum value at the vertex and increases as x moves further from 0.

By practicing graph interpretation, you’ll develop a deeper understanding of functions and their behaviors, which is critical for solving more advanced mathematical problems.

Quadratic Equations in Algebra 2

Quadratic equations play a central role in higher-level mathematics. These equations, which involve squared variables, describe various phenomena in fields such as physics, engineering, and economics. Understanding how to solve and manipulate quadratic equations is crucial for progressing in mathematics. In this section, we will explore methods for solving quadratic equations and understanding their properties.

Methods for Solving Quadratic Equations

There are several techniques for solving quadratic equations, each suited for different types of problems. The most common methods include:

Factoring: This method involves expressing the quadratic equation as a product of binomials. It’s effective when the equation can be easily factored into simple terms.
Quadratic Formula: The quadratic formula is a general method that can be used to solve any quadratic equation. It is given by x = (-b ± √(b² – 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation ax² + bx + c = 0.
Completing the Square: This method involves manipulating the equation so that one side becomes a perfect square trinomial, making it easier to solve for x.

Understanding the Graph of a Quadratic Equation

The graph of a quadratic equation is a parabola, which can open either upward or downward depending on the sign of the leading coefficient (a). The vertex of the parabola represents the maximum or minimum point of the function. Here are some key features of the graph:

Vertex: The vertex is the point where the parabola changes direction. It can be found using the formula x = -b / 2a to determine the axis of symmetry.
Axis of Symmetry: This is the vertical line that divides the parabola into two symmetrical halves. It always passes through the vertex.
Roots or Zeros: These are the x-values where the graph intersects the x-axis. They represent the solutions to the quadratic equation and can be found by factoring, using the quadratic formula, or graphing.

Mastering quadratic equations allows students to solve real-world problems involving projectile motion, optimization, and many other applications. By practicing different solution methods and analyzing their graphs, you will gain a strong foundation in solving quadratic problems with confidence.

Polynomials and Their Solutions

Polynomials are mathematical expressions consisting of variables and coefficients, linked by addition, subtraction, and multiplication operations. These expressions can model a wide range of real-world situations, from physics to economics, and are essential for understanding more complex mathematical concepts. The solutions to polynomial equations, also known as the roots, are fundamental in solving various types of problems across different fields.

Types of Polynomial Equations

Polynomial equations can vary in complexity, depending on the degree of the polynomial. The degree refers to the highest power of the variable in the equation. Common types of polynomials include:

Linear Polynomials: These polynomials have the form ax + b = 0, where the degree is 1. They represent straight lines and are the simplest type of polynomial.
Quadratic Polynomials: These equations involve a squared term, such as ax² + bx + c = 0, and represent parabolic curves.
Cubic and Higher-Degree Polynomials: These equations involve terms with powers higher than 2 and may produce more complex graphs, including curves with multiple turning points.

Finding Solutions to Polynomial Equations

The solutions to polynomial equations, or the values of the variable that make the equation true, can be found using several methods:

Factoring: If the polynomial can be factored, the solutions can be found by setting each factor equal to zero and solving for the variable.
Graphing: By graphing the polynomial, the points where the curve crosses the x-axis represent the real solutions to the equation.
Rational Root Theorem: This theorem provides a systematic way to find potential rational roots of the polynomial equation. Testing these roots can help find the actual solutions.
Numerical Methods: In cases where factoring or other methods are difficult, numerical techniques such as Newton’s method can be used to approximate the solutions.

Understanding polynomials and how to find their solutions is crucial for solving many advanced mathematical problems. Mastering these techniques opens the door to tackling more complex equations and applications in various scientific and engineering fields.

Rational Expressions in Algebra 2

Rational expressions are mathematical expressions that involve fractions, where both the numerator and the denominator are polynomials. These types of expressions can often be simplified, manipulated, and solved just like regular fractions, but they come with unique challenges, such as restrictions on the values that variables can take. Understanding rational expressions is crucial for solving more complex equations and working with advanced mathematical concepts.

To work with rational expressions effectively, it’s important to first recognize how to simplify them. Simplification involves factoring the numerator and denominator and canceling out any common factors. This process makes the expression easier to handle and often reveals solutions or behaviors that might not be immediately obvious. However, when simplifying, one must always remember to check for domain restrictions to avoid division by zero.

Another key concept is performing operations with rational expressions. Just as with fractions, you can add, subtract, multiply, and divide rational expressions. Each operation comes with its own set of rules, such as finding a common denominator for addition and subtraction or cross-multiplying for division. These operations are foundational in solving equations involving rational expressions and can help in simplifying complex problems.

In addition to simplifying and performing operations, rational expressions are often used in real-world problems. They model various situations, such as rates, ratios, and proportional relationships. Mastering the manipulation of these expressions allows you to solve a wide range of problems in fields like physics, engineering, and economics.

Using Real-World Examples in Algebra 2

Mathematics becomes more meaningful when it can be applied to real-world scenarios. By using practical examples, abstract concepts gain clarity, allowing students to see the relevance of what they’re learning. In advanced problem-solving, such as with equations and functions, it’s important to connect theory to tangible situations, whether it’s for analyzing financial trends, understanding motion in physics, or predicting outcomes in various fields.

Real-world applications provide opportunities to explore complex ideas in a way that makes sense outside of the classroom. For example, linear equations can model the relationship between time and distance, while quadratic equations may be used to predict the path of an object in motion. Similarly, rational expressions can represent rates and proportions that occur in daily life, such as the speed of a vehicle or the efficiency of a machine.

Common Applications of Mathematical Concepts

Here are some common examples where mathematical expressions are used to solve real-world problems:

Concept	Real-World Application
Linear Equations	Used to model relationships between variables, such as calculating the cost of a service based on time or quantity.
Quadratic Functions	Commonly used to predict the trajectory of objects, such as in physics when analyzing projectile motion.
Exponential Growth and Decay	Used to model population growth, radioactive decay, or the depreciation of assets over time.
Rational Expressions	Help solve problems involving rates, such as determining the speed of a vehicle or calculating the efficiency of a process.

Understanding how mathematical principles apply to real-life scenarios not only deepens comprehension but also enhances problem-solving skills. By seeing how these concepts work in practice, students can better appreciate the value of learning advanced mathematical techniques and how they can be used to tackle everyday challenges.

How to Improve Your Algebra Skills

Strengthening your mathematical abilities requires consistent practice and understanding the key concepts that form the foundation of problem-solving techniques. Whether you’re tackling equations, working with functions, or analyzing data, improving your skills involves more than just memorization – it requires critical thinking and a strategic approach to learning.

To build a solid grasp of mathematical principles, it’s important to approach each topic with focus and break down complex problems into manageable steps. The following strategies can help you enhance your proficiency and boost your confidence when solving math problems.

Effective Study Techniques

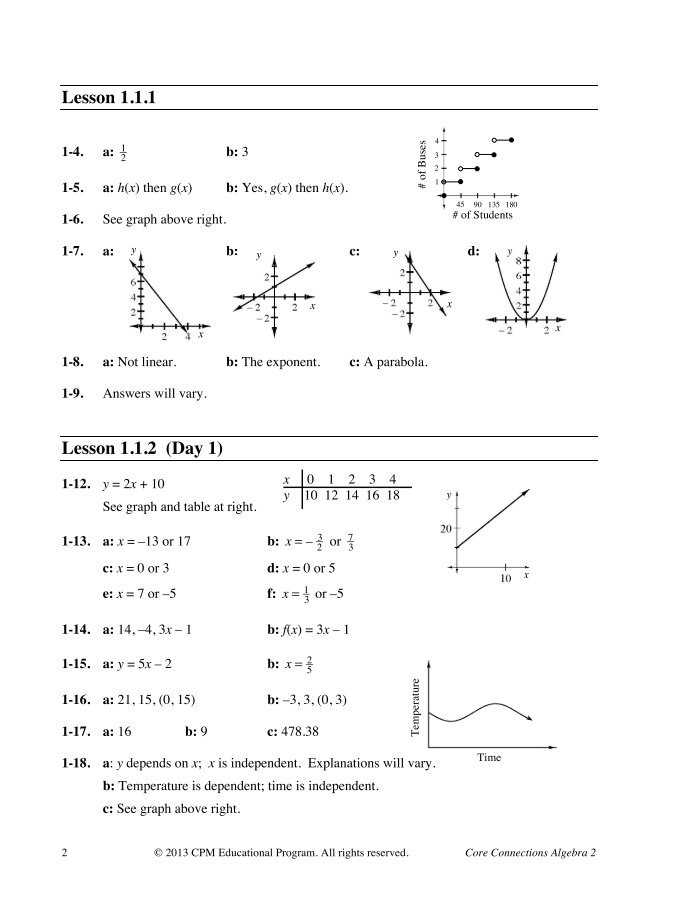
Practice Regularly: Consistency is key when mastering mathematical techniques. Set aside time each day to practice different types of problems, from basic to more advanced.
Understand the Concepts: Focus on understanding the underlying principles rather than just memorizing formulas. This deeper understanding will help you tackle a wider range of problems.
Use Resources: Take advantage of study guides, online tutorials, and textbooks to gain a variety of perspectives on problem-solving methods.
Ask for Help: Don’t hesitate to seek guidance from teachers, tutors, or peers when you encounter difficulties. Explaining your thought process can often help clarify your understanding.
Work in Groups: Collaborating with others provides an opportunity to learn different approaches to solving problems and reinforces your own knowledge.

Common Mistakes to Avoid

Skipping Steps: It’s tempting to rush through problems, but skipping steps can lead to mistakes. Always follow each step methodically to ensure accuracy.
Ignoring the Basics: Neglecting foundational concepts can create gaps in your knowledge. Make sure to revisit earlier topics if you’re struggling with more advanced ones.
Overlooking Details: Pay attention to signs, parentheses, and other small details in equations. Small mistakes can lead to larger errors in the final solution.

By implementing these strategies and maintaining a consistent study routine, you’ll gradually see improvements in your problem-solving ability and mathematical confidence. Mastery comes with practice, and each step forward will make tackling more challenging concepts that much easier.

Path to Success in Advanced Mathematics

Mastering mathematical concepts is a key step toward academic success, particularly when dealing with advanced topics. To excel, it’s important to understand the essential principles, develop effective problem-solving strategies, and approach learning with a disciplined mindset. Focusing on foundational skills while building upon them gradually will equip you with the tools needed to tackle increasingly complex tasks.

Success in this subject comes from a blend of practice, understanding, and application. Whether you are dealing with expressions, equations, or advanced functions, breaking down problems into smaller parts and tackling them step by step will build both confidence and competence. Below are a few ways to set yourself up for achievement in your studies.

Key Strategies for Mastery

Focus on Understanding: Rather than memorizing formulas or solutions, ensure you understand the rationale behind each step. This deeper comprehension allows you to apply knowledge to new problems.
Practice Consistently: Set aside time each day for focused practice. Regular repetition strengthens your skills and helps you identify patterns and common strategies in problem-solving.
Review Mistakes: Take the time to analyze errors and understand where you went wrong. This reflection process is a powerful learning tool that enhances long-term retention.
Utilize Available Resources: Leverage textbooks, online tutorials, or peer study groups to reinforce concepts and gain fresh perspectives. Collaboration often leads to a better understanding of the material.

Building Confidence and Proficiency

Start with the Basics: Ensure a solid foundation by revisiting earlier material. A strong grasp of the fundamentals makes learning more advanced topics easier and less stressful.
Work on Problem-Solving Skills: Solve a variety of problems, from the simplest to the more complex. This helps you develop flexibility in applying different techniques to different scenarios.
Stay Organized: Keep track of formulas, important steps, and concepts in a notebook or digital document. An organized approach reduces the risk of overlooking key elements in problem-solving.

By adopting these strategies, you will build a deeper understanding of advanced mathematical principles and foster the confidence needed to approach challenging topics with ease. A well-rounded approach to studying – focusing on practice, review, and strategic learning – will help you navigate even the most complex mathematical problems successfully.