June 2015 Geometry Regents Exam Answer Key

Success in high school assessments relies on understanding key concepts and applying problem-solving techniques effectively. These evaluations test a wide range of mathematical principles, from basic calculations to more complex logical reasoning. Grasping these ideas helps students not only in their current studies but also prepares them for future academic challenges.

Solving problems efficiently requires a solid foundation in the core topics presented in the test. By reviewing previous assessments, students can pinpoint recurring themes and strategies that are commonly tested. This approach ensures a more targeted and effective review process, boosting confidence and performance.

Detailed breakdowns of past problem sets provide a valuable opportunity to revisit the methodologies used to reach correct solutions. Understanding why certain answers work, and others do not, is crucial for mastering the material. Such insights encourage a deeper understanding and reinforce essential skills necessary for tackling similar questions in future evaluations.

June 2015 Geometry Regents Exam Answers

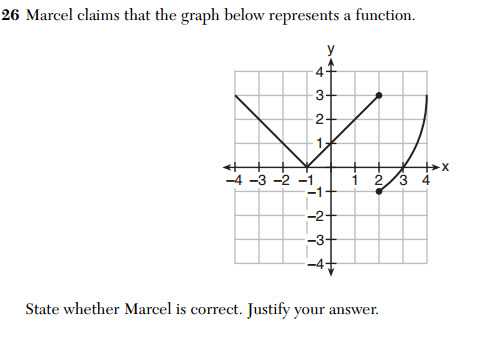
Reviewing the results of a key academic assessment is an essential step in understanding the material and improving performance in future tests. By examining previously administered tests, students gain valuable insight into the types of questions commonly posed and the strategies used to answer them correctly. This process allows learners to identify strengths and areas that need further attention.

Breaking down the problem-solving process is crucial for mastering the techniques necessary to succeed. Each question in the evaluation presents an opportunity to apply mathematical principles to real-world scenarios. By analyzing the steps that lead to the correct solution, students can refine their approach and build greater confidence in their problem-solving abilities.

Reviewing step-by-step solutions helps to highlight the logical sequence required to tackle complex questions effectively. Understanding how to break down each problem into manageable parts ensures that learners can navigate even the most challenging problems with ease. Additionally, this practice strengthens critical thinking skills and prepares students for future assessments where similar challenges may arise.

Overview of June 2015 Exam

The assessment in question tests a wide range of skills, focusing on various mathematical concepts that are essential for academic development. Students are required to apply their knowledge to solve problems that test their understanding of core principles. The structure of the test is designed to challenge learners’ abilities to think critically and logically while adhering to specific problem-solving strategies.

Section	Topics Covered	Question Types
Part 1	Basic calculations and formulas	Multiple Choice
Part 2	Problem-solving and reasoning	Short Answer
Part 3	Proofs and logical arguments	Extended Response

Understanding the breakdown of question types and the topics covered helps students focus on key areas of study. Each section is carefully crafted to test different aspects of mathematical thinking, from simple computations to more intricate logical reasoning. This variety in the question format ensures that students are prepared for all potential scenarios and can demonstrate their proficiency across multiple levels of complexity.

Importance of Regents Geometry Exam

This assessment plays a crucial role in evaluating a student’s grasp of essential mathematical concepts. It serves as a benchmark for understanding key principles and is an important indicator of readiness for higher-level academic challenges. By testing a wide range of problem-solving abilities, this evaluation helps students demonstrate their understanding and logical reasoning skills in a structured manner.

Strengthens critical thinking abilities
Enhances problem-solving skills across various topics
Provides a foundation for future academic success
Encourages mastery of fundamental mathematical principles

Beyond academic knowledge, this assessment also holds significant weight in determining graduation requirements. Its results often influence future opportunities, including college admissions and scholarship eligibility. As such, preparing thoroughly for this type of test is vital for academic advancement and long-term educational goals.

Understanding key concepts ensures success in further studies
Mastering techniques improves performance on future tests
Consistent preparation builds confidence and reduces test anxiety

Key Topics Covered in Geometry Exam

The assessment evaluates a wide array of mathematical principles, each designed to challenge students’ understanding and application of core concepts. These topics are essential for building a solid foundation in problem-solving, logical reasoning, and critical thinking. By mastering these areas, students are equipped to approach complex problems with confidence and precision.

Fundamental Mathematical Principles

Among the most critical concepts tested are basic calculations, geometric relationships, and theorems that form the backbone of more advanced topics. These include operations on shapes, understanding spatial properties, and the ability to apply abstract principles to real-world situations.

Advanced Problem-Solving Techniques

In addition to basic principles, students are also assessed on their ability to solve intricate problems involving reasoning and logical deduction. These questions require a deeper understanding of the material, including the ability to work through proofs and construct logical arguments to justify solutions.

Topic	Skills Tested	Question Types
Shapes and Properties	Identification, calculation of areas, volumes	Multiple Choice, Short Answer
Proofs and Theorems	Logical reasoning, constructing proofs	Extended Response
Coordinate Geometry	Plotting points, equations of lines	Multiple Choice, Short Answer
Transformations	Understanding translations, rotations, reflections	Short Answer

Familiarity with these key topics is essential for performing well on the assessment. Mastering the underlying principles and applying them effectively will not only improve scores but also strengthen students’ overall mathematical reasoning abilities.

How to Approach Geometry Regents Questions

When tackling a set of problems on a math assessment, it is important to follow a structured approach that ensures accuracy and efficiency. By breaking down each question methodically, students can better organize their thoughts, apply appropriate strategies, and reach the correct solution in a timely manner. This approach not only helps in maximizing performance but also reduces the likelihood of errors under time constraints.

Steps to Approach Problems

Start by carefully reading each question to ensure full understanding. Focus on the key information provided and the specific requirements of the problem. It is important to identify the most relevant principles or formulas that will help solve the problem.

Read the question carefully to identify what is being asked
Highlight or underline key data points and variables
Determine the most appropriate method or formula to apply
Work through the problem step by step, showing all calculations
Double-check your results to ensure accuracy

Time Management and Strategy

Efficiently managing time during the assessment is just as important as solving the problems correctly. Prioritize questions based on difficulty level and allocate enough time for each section. Don’t get stuck on a single challenging question–move on and return to it if time allows.

Begin with questions that seem easier or more familiar
Leave more difficult problems for later, but don’t ignore them
Make sure to review the entire set of questions before finalizing answers

By maintaining a focused, step-by-step approach, students can confidently tackle even the most difficult problems. Using these strategies effectively allows for better time management and enhances problem-solving accuracy across the entire test.

Understanding Multiple Choice Format

The multiple choice format is a common testing method used to assess a student’s understanding of various topics. It presents a question with several possible answers, only one of which is correct. This format tests not only knowledge but also decision-making skills, as students must evaluate all the options carefully before selecting the most accurate response.

Key Features of Multiple Choice Questions

In this type of question, students are typically given four or five answer choices. While the incorrect options, or “distractors,” may seem plausible, there is always one clear and correct answer. The challenge lies in distinguishing between the right answer and those that are designed to mislead or confuse.

Clarity of the Question: Ensure the question is fully understood before considering the choices.
Identifying Distractors: Pay close attention to the wording of each option, as the distractors are often subtly misleading.
Elimination Strategy: Narrow down the options by eliminating answers that are clearly wrong, increasing the odds of selecting the right one.

Best Strategies for Multiple Choice Questions

Reading all options carefully is crucial to making the correct choice. Even if one answer appears to be correct at first glance, it’s important to examine all choices before finalizing your answer. Additionally, if you’re unsure, consider reasoning through the problem to rule out implausible options and increase your chances of selecting the correct one.

Don’t rush–take time to read each choice thoroughly.
If stuck, eliminate at least one or two wrong answers to improve your chances.
If needed, revisit difficult questions after completing the easier ones.

By mastering these strategies, students can approach multiple choice questions with more confidence and accuracy, improving their chances of success on the test.

Tips for Solving Geometry Proofs

Solving proofs in mathematics requires a logical approach, attention to detail, and a clear understanding of the principles involved. The goal is to demonstrate the validity of a statement by using known facts, theorems, and logical reasoning. The process can seem challenging, but with the right strategies, it becomes more manageable and systematic.

One of the most important steps when working on proofs is to carefully analyze the given information and what needs to be proved. This helps to determine the necessary steps and identify the appropriate theorems or properties to apply. Here are a few essential tips to keep in mind when tackling these types of problems:

Start with the Given Information: Make sure to identify all the data provided in the problem. This includes any points, angles, or relationships that are directly given or implied.
Work from What You Know: Build upon the facts you already understand. Use previously proven theorems, properties, and definitions to progress step by step.
Draw Diagrams: Visualizing the problem can be incredibly helpful. Even if the problem provides a diagram, creating your own can give you a clearer understanding of the relationships involved.
Logical Flow: Each step in a proof must be logically connected to the previous one. Avoid jumping to conclusions and ensure each step follows from the last.
Conclude Clearly: Finish with a clear conclusion that directly addresses the statement to be proven, ensuring all steps lead logically to this conclusion.

By following these strategies and practicing regularly, students can improve their ability to solve proofs and build stronger problem-solving skills. The key to success lies in methodically breaking down the problem and using logical steps to reach a solid conclusion.

Common Mistakes to Avoid in Geometry

Mathematical problems involving shapes and their properties can be tricky, especially when the focus is on precise calculations and logical reasoning. Students often make certain errors that can lead to incorrect solutions, even when they understand the concepts. Recognizing these common mistakes and knowing how to avoid them can significantly improve problem-solving accuracy.

Many errors occur when students rush through the problem-solving process, skip important steps, or overlook crucial details. It’s essential to slow down, read each question carefully, and stay focused on the relationships between various elements in a problem. Here are some of the most frequent mistakes students make:

Misinterpreting the Question: Failing to understand what is being asked can lead to incorrect solutions. Always take time to clearly define the question before starting the solution process.
Incorrect Application of Formulas: Using the wrong formula or applying it incorrectly is a common error. Make sure to select the appropriate formula for the given situation and check each variable before solving.
Skipping Steps: Omitting steps in calculations or reasoning can lead to missing key details. Always show your work and ensure that each step logically leads to the next.
Confusing Similar Concepts: Some concepts may seem similar but differ significantly in application. For instance, confusing properties of parallel lines with those of perpendicular ones can result in errors in reasoning.
Not Using a Diagram: Visualizing the problem is essential, especially for complex problems. Failing to draw or reference a diagram can lead to missed relationships between different elements of the problem.

By being aware of these mistakes and applying a careful, methodical approach to each problem, students can greatly improve their chances of solving problems correctly. Practicing regularly and paying attention to detail will help avoid these pitfalls and enhance overall problem-solving skills.

Step-by-Step Solutions to Exam Questions

Breaking down complex problems into smaller, manageable steps is key to mastering challenging questions. By approaching each question methodically, students can ensure they do not overlook important details and that they apply the correct strategies. Step-by-step solutions provide a clear path from the initial problem to the final result, making the process less intimidating and more organized.

Breaking Down the Problem

Before attempting to solve any problem, it’s essential to read through the question carefully. Identify the given information and the goal of the problem. Once you understand what is being asked, organize the data in a way that makes sense, such as drawing diagrams or listing out known variables.

Identify key information and variables.
Determine the goal or the unknown value you need to solve for.
Visualize the problem by creating a diagram, if applicable.

Step-by-Step Process

Start solving the problem one step at a time. Avoid jumping ahead or making assumptions without justification. Each step should logically follow from the previous one, ensuring accuracy. It’s helpful to write out each calculation and explanation, as this makes it easier to identify errors if something doesn’t work out as expected.

Apply relevant formulas or principles.
Perform calculations and show all steps clearly.
Double-check each step before moving on to the next one.
Revisit the final solution and ensure it answers the original question.

By following this structured approach, students can tackle even the most complex problems with confidence. Step-by-step solutions not only help ensure accuracy but also improve overall problem-solving skills for future assessments.

Geometry Formulas You Must Know

Having a solid grasp of essential mathematical equations is critical when working with shapes, angles, and measurements. These formulas form the foundation for solving a wide variety of problems, and understanding how to apply them effectively can greatly enhance your problem-solving abilities. Memorizing these formulas and knowing when and how to use them is a vital step in mastering the subject.

Key Formulas for Shapes and Areas

Different shapes come with their own set of formulas, each designed to calculate properties such as area, perimeter, and volume. Familiarity with these key equations is necessary for accurately solving problems related to both two-dimensional and three-dimensional figures.

Area of a Rectangle: Area = Length × Width
Perimeter of a Rectangle: Perimeter = 2(Length + Width)
Area of a Triangle: Area = ½ × Base × Height
Area of a Circle: Area = π × Radius²
Volume of a Rectangular Prism: Volume = Length × Width × Height

Important Theorems and Properties

Along with basic formulas, there are key theorems and properties that are indispensable when working with shapes. These allow for deeper analysis and problem-solving in geometry-related questions, especially those that require proof or reasoning.

Pythagorean Theorem: a² + b² = c² (for right triangles)
Angle Sum Property of Triangles: Sum of angles in a triangle = 180°
Sum of Interior Angles of a Polygon: Sum = (n – 2) × 180°, where n = number of sides
Volume of a Sphere: Volume = 4/3 × π × Radius³

By mastering these formulas and understanding their application, you will be better prepared to approach a wide range of mathematical challenges with confidence. These foundational equations are crucial for solving not just basic problems but also more complex scenarios involving proofs and calculations.

Analyzing June 2015 Regents Answers

Breaking down the solutions from past assessments is a valuable exercise in understanding common patterns and the reasoning behind correct answers. Analyzing the responses allows students to identify the most effective strategies for approaching similar questions, reinforcing their understanding of key concepts. By reviewing these solutions, one can gain insights into both the methods used and potential pitfalls to avoid during problem-solving.

Key Strategies for Successful Problem Solving

When evaluating responses from previous tests, it’s crucial to understand the strategies that lead to accurate results. This includes knowing which formulas to apply, how to structure the solution step by step, and when to use logical reasoning to check your work. Identifying these strategies will help build a strong foundation for future assessments.

Recognizing when to apply basic mathematical rules and formulas.
Breaking down multi-step problems into simpler parts.
Cross-checking answers for consistency with the given information.

Common Mistakes to Avoid

Analyzing past solutions also sheds light on frequent errors made during problem-solving. Whether it’s misinterpreting a question, making calculation mistakes, or overlooking key information, understanding these common pitfalls helps students avoid repeating them. It’s important to carefully review every step and ensure all the conditions are met before finalizing an answer.

Failing to double-check calculations.
Misunderstanding the question’s requirements.
Overlooking necessary steps or assumptions in reasoning.

By reviewing and analyzing the solutions to past problems, students can refine their problem-solving techniques and be better prepared for similar challenges in the future. The ability to recognize both effective strategies and common mistakes is key to improving performance on future assessments.

Problem Type	Common Strategy	Frequent Mistakes
Algebraic Manipulation	Apply appropriate formulas, simplify step by step.	Skipping steps, calculation errors.
Proofs	State given information clearly, work through logical steps.	Omitting reasoning, unclear conclusions.
Word Problems	Translate the problem into an equation, solve systematically.	Misinterpreting the question, ignoring units.

How to Improve Your Geometry Score

Improving your performance in mathematical assessments requires a combination of strategy, practice, and focused learning. Understanding the fundamental concepts and applying them to problem-solving situations is key to boosting your score. Consistent preparation, along with targeted practice on areas of difficulty, will help reinforce knowledge and enhance overall test-taking skills.

Effective Study Strategies

To see significant improvement, it’s important to approach studying with a clear and systematic plan. Breaking down topics into manageable sections allows for focused learning, while regular review ensures that material stays fresh in your mind.

Set aside dedicated study time each week to review concepts.
Work on practice problems to solidify your understanding.
Focus on mastering one concept before moving on to the next.

Maximizing Practice and Review

Regular practice is essential for mastering any subject. By practicing a variety of problems, especially those that challenge you the most, you build confidence and improve problem-solving speed. Reviewing incorrect solutions is equally important, as it allows you to understand mistakes and avoid repeating them.

Use past practice tests to simulate real test conditions.
Review solutions to understand mistakes and correct them.
Identify common problem types and practice them regularly.

Additional Tips for Success

There are a number of other techniques that can further improve your score. Staying organized, managing your time effectively during practice, and learning from others are all strategies that contribute to success.

Organize notes and formulas for easy access during review.
Work on time management to improve efficiency in problem-solving.
Join study groups or seek help from a tutor for personalized guidance.

By incorporating these strategies into your study routine, you’ll be able to improve your understanding and confidence, ultimately leading to a higher score on any related assessment.

Preparing for the Geometry Regents Exam

Effective preparation for a mathematics assessment involves a combination of consistent practice, understanding core principles, and mastering problem-solving techniques. By dedicating sufficient time and focusing on the key areas of the subject, you can build the confidence and knowledge needed to succeed. A structured approach to reviewing material, coupled with hands-on practice, is essential for mastering the skills required for the test.

Start by organizing your study schedule, allocating time for each topic based on its importance and difficulty level. It’s crucial to focus on areas where you might struggle the most, but also to maintain a balance by reviewing all the relevant material. Additionally, practice is essential to reinforce your understanding and develop efficient problem-solving strategies. By continuously assessing your progress through practice tests, you can identify weak points and adjust your study plan accordingly.

Incorporating a variety of study resources, including textbooks, online materials, and practice problems, can also provide a well-rounded understanding of the subject. Whether you prefer working individually or in a group setting, engaging with the material from different perspectives will enhance your ability to retain and apply the information.

Finally, maintaining a positive mindset throughout the preparation process is vital. Staying focused, avoiding stress, and managing time effectively will help you approach the assessment with confidence, ensuring the best possible performance.

Strategies for Answering Word Problems

Word problems can often seem daunting, but with the right approach, they become much easier to solve. The key to tackling these problems is breaking them down into manageable steps and focusing on understanding what the question is asking. By carefully analyzing the information provided and organizing your thoughts, you can systematically find the solution.

1. Read Carefully and Highlight Key Information

The first step in solving any word problem is to read it thoroughly. Take note of the important details and underline or highlight key numbers, relationships, and phrases. This will help you identify what is known and what needs to be determined. Pay close attention to units of measurement, as they can often play a critical role in the solution.

2. Translate the Words into Mathematical Expressions

Once you’ve gathered the relevant information, the next step is to translate the word problem into a mathematical equation or expression. Identify the variables and use appropriate symbols for operations such as addition, subtraction, multiplication, or division. This step is essential for making the problem solvable using mathematical methods.

3. Solve the Equation Step by Step

Now that you have a mathematical expression, proceed to solve it step by step. Simplify the equation where possible, and keep track of your work to avoid mistakes. It’s also helpful to check if your answer makes sense in the context of the problem as you go along.

4. Double-Check Your Work

Before finalizing your answer, take a moment to review each step. Ensure that you’ve accounted for all of the information in the problem and that your solution is reasonable. Double-check calculations and verify that the units of measurement match the requirements of the problem.

By following these strategies, you can approach word problems with confidence and improve your ability to solve them accurately. Practicing these steps regularly will help you become more efficient and reduce the chances of making errors under pressure.

Resources for Geometry Exam Review

Preparing for an important assessment can be challenging, but using the right resources can make the process much more efficient. There are various materials available to help you review key concepts, practice solving problems, and refine your skills. Whether you prefer interactive tools, textbooks, or online courses, there’s something for every learning style.

Here are some of the most valuable resources you can use for your preparation:

Practice Tests: Taking practice tests is one of the most effective ways to evaluate your knowledge and improve your problem-solving speed. Many websites and educational platforms offer free practice tests that mimic the format and difficulty level of the actual assessment.
Interactive Online Platforms: Websites with interactive lessons and quizzes can help reinforce concepts and provide instant feedback. Platforms like Khan Academy, Coursera, and other educational tools offer a wide range of exercises tailored to different topics and difficulty levels.
Study Guides and Workbooks: Comprehensive study guides and workbooks often provide detailed explanations of key concepts, as well as plenty of practice problems to solve. These books can be found at libraries, bookstores, or online retailers.
YouTube Tutorials: For visual learners, YouTube offers an abundance of tutorials and step-by-step guides. Channels dedicated to mathematics education provide in-depth explanations of complex topics and offer helpful tips for solving challenging questions.
Flashcards: Flashcards are an excellent tool for memorizing formulas, key terms, and properties. You can create your own set or find pre-made flashcards online that cover the most essential material for your review.
Group Study Sessions: Joining or organizing a study group allows you to discuss difficult topics with peers, share resources, and learn from each other. Group study can help clarify any areas of confusion and provide new insights into solving problems.

Using a combination of these resources will allow you to approach your review from multiple angles, boosting both your confidence and competence. Make sure to allocate enough time to explore each resource and assess your progress regularly.

Common Geometry Topics on Regents Exam

Assessments focused on mathematical concepts often cover a wide range of topics, ensuring that students demonstrate their understanding of various principles and techniques. In this section, we will explore the most frequently encountered subjects, which are essential for success in any related test. Mastering these topics will give you a strong foundation to tackle problems effectively and efficiently.

Key Areas of Focus

Among the many topics that may appear, there are a few that consistently show up due to their foundational importance. These areas require not only theoretical knowledge but also the ability to apply principles in different contexts. Here are the major categories to review:

Properties of Shapes and Figures: This includes understanding the characteristics of common geometric shapes such as triangles, quadrilaterals, and circles. You should be comfortable with concepts such as angles, parallel lines, congruency, and symmetry.
Coordinate Geometry: In this area, you will work with points on a coordinate plane, calculating distances, midpoints, and slopes. Mastery of the distance and midpoint formulas is key to solving related problems.
Proofs and Theorems: Logical reasoning and the ability to prove statements using deductive methods are essential. Familiarize yourself with fundamental theorems and postulates, such as the Pythagorean Theorem and angle relationships.
Transformations and Symmetry: Topics like translations, rotations, reflections, and dilations are critical for understanding how figures can change positions and sizes while maintaining certain properties.
Surface Area and Volume: Calculating the surface area and volume of three-dimensional objects is an important skill, especially for shapes like spheres, cylinders, cones, and prisms.
Trigonometry Basics: Some level of trigonometry is often included, particularly in solving for unknown sides or angles in right triangles using sine, cosine, and tangent ratios.

Effective Review Tips

Once you identify the topics that appear most frequently, focus your study efforts on mastering these areas. Practice solving problems and applying formulas to various scenarios. Utilize online resources, textbooks, and practice tests to deepen your understanding. With dedication and consistent practice, you’ll be well-equipped to handle any problem that comes your way.

How to Use Practice Tests Effectively

Practice tests are an essential tool for any student preparing for a major assessment. They provide a valuable opportunity to familiarize oneself with the types of questions likely to appear, while also helping to build confidence and time-management skills. However, simply completing practice questions is not enough. To maximize their effectiveness, a strategic approach is necessary.

Set Clear Goals Before Each Test

Before taking a practice test, it is important to set specific objectives. Decide what you aim to achieve–whether it’s improving your time management, mastering certain topics, or simply getting a sense of your strengths and weaknesses. Here are a few tips to help structure your practice sessions:

Focus on Weak Areas: If you’ve struggled with specific concepts, dedicate time to those areas during your practice tests. This targeted approach helps to strengthen areas that need the most improvement.
Simulate Test Conditions: Try to replicate the actual testing environment as closely as possible. Set a timer, avoid distractions, and take the test in one sitting to get used to working under time constraints.
Track Your Progress: Keep track of your scores and review your mistakes. This will help you identify patterns in the types of questions you tend to get wrong, allowing you to adjust your study methods accordingly.

Analyze Results After Completing the Test

Once you’ve finished a practice test, the real work begins. Simply taking the test is not enough; you need to spend time analyzing your results. Review both the correct and incorrect answers carefully to understand why you made mistakes. Here are steps to follow:

Understand the Mistakes: For each incorrect answer, take the time to understand why you got it wrong. Was it due to a misunderstanding of the concept, a calculation error, or a time-management issue?
Review Relevant Content: If you missed questions in a particular topic, review the material associated with it. Practice more problems on that subject until you feel confident.
Adjust Your Strategy: Based on your analysis, make adjustments to your study plan. Focus more on areas where you struggled and consider changing your approach to problem-solving if necessary.

By using practice tests in a thoughtful and strategic manner, you can greatly improve your performance. They not only help you get used to the format and timing but also provide invaluable insights into your strengths and areas for improvement.

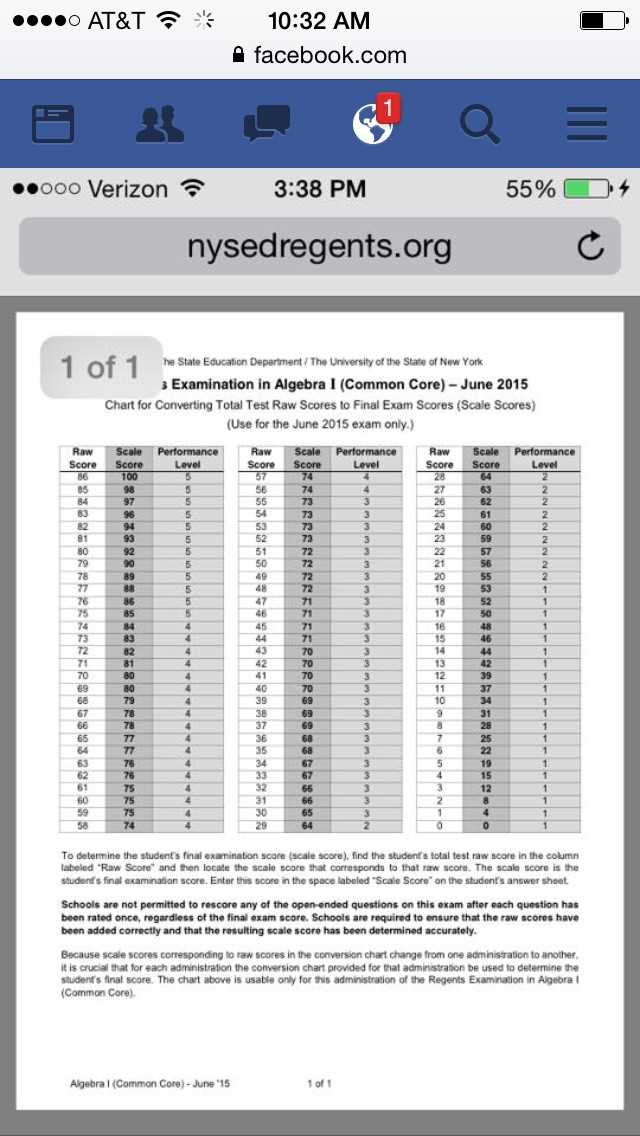
Understanding the Grading System

Understanding how your performance is evaluated is crucial for effectively preparing for any assessment. A clear grasp of the grading structure helps you focus on the right areas, manage your time efficiently, and set realistic expectations. Each test typically uses a specific system to assess the quality of your work, and knowing how these criteria are applied can improve your chances of success.

Key Components of the Grading Scale

While grading systems can vary, most follow a similar structure that includes several key components. Here are the general factors that influence your overall score:

Raw Score: This is the total number of correct answers you provide. It is the first step in determining your score and helps establish your baseline performance.
Scaled Score: Often, the raw score is adjusted to a standardized scale. This process accounts for different versions of the test and ensures fairness across different administrations.
Weighted Questions: Some questions may carry more weight than others. For example, complex problem-solving questions may be worth more points than simpler recall-based questions. Make sure to prioritize high-weight sections during your preparation.

How to Interpret the Final Score

Once your raw score is converted into a scaled score, it is important to understand what that number means in relation to your overall performance. Here’s a breakdown:

Passing Score: Typically, a certain scaled score is required to pass. Understanding this threshold helps you assess your performance and adjust your study plan accordingly.
Score Range: Depending on the difficulty of the test, scores may vary. Knowing the range and how the scores are distributed can help you understand where you stand in comparison to others.
Feedback: In some systems, additional feedback or commentary may be provided alongside your score. This can highlight specific areas where you excelled or struggled.

By familiarizing yourself with the grading system, you can approach the assessment with greater confidence and clarity. It also helps you to identify areas that need more attention, ensuring that you focus your efforts on what truly impacts your overall score.