
Mathematical studies often present unique challenges for learners, requiring both critical thinking and practical application. Success in this area depends on a clear understanding of principles and the ability to apply them effectively in problem-solving scenarios. Students and educators alike benefit from tools and strategies that simplify this learning process.
Resources designed for academic improvement can help bridge knowledge gaps and enhance comprehension. By using tailored materials and engaging exercises, learners can build confidence and proficiency in solving complex problems. This approach not only supports educational goals but also fosters a deeper appreciation for the subject’s relevance in everyday life.
To achieve these objectives, it is essential to identify reliable materials and effective study techniques. Combining structured guidance with interactive learning methods can make a significant difference, ensuring a well-rounded and practical approach to mastering core topics.
Understanding Key Concepts in the Curriculum
In academic programs focused on spatial reasoning, students are expected to grasp a range of foundational concepts that will support their progression in higher-level mathematics. These concepts build upon one another, creating a structured learning path that enhances both understanding and problem-solving skills. By mastering core ideas early on, students develop a strong foundation that prepares them for more complex challenges.
The curriculum aims to help learners explore relationships between shapes, measurements, and their properties, with an emphasis on both theory and practical applications. Throughout their studies, students encounter topics that focus on real-world connections, preparing them for careers in fields such as engineering, architecture, and computer science.
Core topics typically covered include:
- Measurement and calculation of angles
- Properties of two-dimensional and three-dimensional shapes
- Understanding transformations and symmetry
- Analyzing relationships between different geometric figures
- Applying theorems and postulates to solve problems
These subjects not only sharpen analytical skills but also promote the ability to reason logically and draw conclusions based on evidence. As students advance, they learn to manipulate abstract concepts and engage in more sophisticated problem-solving techniques.
How to Solve Geometry Problems Efficiently
Mastering mathematical challenges requires a clear plan and logical thinking. An efficient approach can simplify even the most complex tasks, ensuring accurate results in less time. By focusing on critical steps and leveraging helpful techniques, learners can improve their problem-solving abilities.
Practical Techniques for Problem-Solving
To tackle complex tasks effectively, it’s essential to use structured methods. Follow these steps for better outcomes:
- Understand the problem by identifying key information and objectives.
- Organize known data and relationships in a clear format.
- Create a visual representation, such as a diagram or chart.
- Apply logical rules or relevant formulas to find solutions.
- Verify the answer by reviewing calculations and ensuring it meets the requirements.
Essential Tools for Accuracy

Using the right resources can make solving tasks faster and more precise. Below is a table of tools and their specific uses:
| Tool | Application |
|---|
| Platform | Features |
|---|---|
| Khan Academy | Free video lessons, exercises, and personalized dashboards |
| Quizlet | Interactive flashcards and study sets for various subjects |
| Coursera | Online courses from top universities with certification options |
| EdX | Courses from prestigious institutions with free and paid options |
By choosing well-reviewed and reliable platforms, students can enhance their learning experience and prepare more effectively for exams and assignments.
Practice Exercises for Geometry Students

Consistent practice is key to mastering mathematical concepts and improving problem-solving skills. Engaging with a variety of exercises helps students reinforce their understanding and apply theoretical knowledge to practical situations. By regularly working through challenges, learners develop the confidence to approach complex problems with ease.
To enhance skills in this area, students can tackle exercises that range from basic to advanced levels. These exercises help solidify key concepts such as shapes, measurements, angles, and spatial reasoning. Regular practice also assists in developing speed and accuracy when solving problems.
Below are examples of practice exercises to consider:
- Calculate the area and perimeter of different polygons
- Solve problems involving the properties of circles
- Work with triangles and their various properties (e.g., Pythagorean theorem)
- Apply transformations, such as rotations, reflections, and translations
- Practice coordinate plane problems involving slopes and distances between points
By working through such exercises, students gain the skills necessary to confidently solve a wide range of problems and prepare effectively for exams and assessments.
Common Challenges in Geometry and Solutions
Many students face difficulties when learning spatial concepts and mathematical reasoning. These challenges often stem from abstract ideas, complex calculations, or the need for visualizing shapes and patterns. Identifying common struggles and understanding strategies to overcome them can help students approach these topics with greater confidence and clarity.
Common Struggles in Learning Spatial Concepts
Several areas tend to cause confusion among learners. These challenges, if not addressed, can hinder progress and affect overall performance. Below are a few key obstacles students commonly encounter:
- Difficulty visualizing 3D shapes and their properties
- Misunderstanding angle relationships and theorems
- Problems with calculating areas, volumes, and surface areas of various shapes
- Confusion with coordinate plane problems and equations
Strategies for Overcoming These Challenges
Each of these challenges can be overcome with targeted practice, clear explanations, and the right strategies. By breaking down complex problems into smaller steps, students can build a stronger foundation and gradually improve their skills.
| Challenge | Solution |
|---|---|
| Visualizing 3D shapes | Use physical models, diagrams, or interactive apps to enhance understanding |
| Angle relationships | Practice with real-world examples and diagrams to strengthen conceptual understanding |
| Area and volume calculations | Work through practice problems to gain familiarity with formulas and calculations |
| Coordinate plane problems | Review graphing methods and work on visualizing coordinates to improve accuracy |
With the right approach and consistent practice, these challenges can be transformed into opportunities for improvement, leading to better performance and greater mastery of the subject.
Importance of Geometry in Real Life

Mathematical concepts related to shapes, sizes, and spatial relationships are not only essential in academic settings but also play a crucial role in daily life. Understanding these principles can help individuals make informed decisions, solve real-world problems, and navigate their surroundings more effectively. From architecture to navigation, the applications of these concepts are vast and diverse.
In everyday life, many activities require a solid understanding of spatial relationships and measurements. Whether it’s designing a house, determining the best way to arrange furniture, or planning a trip, these principles are at work. Below are several key areas where this knowledge proves invaluable:
- Architecture and Construction: Accurate measurements and understanding of shapes are fundamental when building structures, ensuring they are both safe and functional.
- Art and Design: Artists and designers often rely on shapes, symmetry, and proportions to create aesthetically pleasing works.
- Engineering: From bridges to vehicles, engineers use spatial reasoning to create functional, efficient, and safe designs.
- Navigation: Whether using a map or GPS, understanding distances, angles, and routes is essential for effective travel.
- Technology: Computer graphics, game development, and virtual reality all require knowledge of spatial relationships to create immersive, realistic experiences.
These examples demonstrate how spatial understanding enhances problem-solving skills and is an integral part of various industries and daily tasks. The more one applies these concepts, the more valuable they become in both professional and personal life.
How to Use Geometry Tools Correctly
Mastering the use of measurement instruments is essential for achieving accurate results in mathematical problem-solving. Each tool has its specific purpose, and when used properly, it can make complex calculations and designs much easier to handle. From rulers to protractors, understanding the correct technique can save time and reduce errors.
Essential Tools for Measuring and Drawing
The most commonly used tools in spatial analysis include:
- Ruler: Used for measuring straight lines or drawing precise straight edges.
- Protractor: An essential tool for measuring and creating accurate angles.
- Compass: Helps in drawing circles and arcs with a fixed radius.
- Set Squares: Used for drawing and measuring right angles and other specific angles.
Tips for Accurate Use
To achieve precision, it is important to follow these tips:
- Ensure that your ruler or measuring tape is aligned properly before taking any measurements.
- When using a protractor, place it correctly at the vertex of the angle to get accurate results.
- For circles, ensure the compass’s point is securely placed before drawing the arc to avoid slippage.
- For set squares, check that they are aligned with the edges of your paper or surface to avoid skewed angles.
By using the right tools in the correct manner, individuals can improve their accuracy and efficiency, whether working on simple calculations or more advanced designs. Taking the time to learn how each tool works will ultimately save time and lead to better results in both academic and practical applications.
Preparing for Texas Geometry Exams
Successfully preparing for geometry exams involves a combination of understanding fundamental concepts, practicing problem-solving techniques, and reviewing previous materials. Whether you’re a high school student in Texas or studying for standardized tests, a focused study plan can significantly boost your confidence and performance on test day.
Creating a Study Schedule

Developing a study schedule is crucial for effective exam preparation. Allocate specific times each week to review topics, practice problems, and take mock exams. Consistency is key, so stick to the schedule and gradually increase your study time as the exam date approaches.
Using Study Resources Wisely
Utilize textbooks, online resources, and practice worksheets to reinforce your learning. Online videos and tutorials can provide additional explanations for complex topics. Make sure to focus on areas where you struggle the most, and don’t hesitate to ask for help from teachers or peers.
Interactive Geometry Activities for Learning
Interactive learning activities provide an engaging way to deepen your understanding of mathematical concepts. By actively participating in hands-on exercises, students can visualize and apply theoretical knowledge in practical scenarios, enhancing both retention and comprehension. These activities are especially useful for mastering challenging topics, as they allow for exploration and experimentation in a fun, dynamic environment.
Benefits of Interactive Learning

Using interactive activities helps develop problem-solving skills and promotes critical thinking. When students are involved in these activities, they become more invested in their learning process, which improves their ability to grasp difficult ideas.
Effective Activities to Try
- Geometry Puzzles: Solving geometric puzzles like tangrams or shape rearrangements encourages spatial reasoning and understanding of geometric properties.
- Virtual Simulations: Online tools that simulate geometric shapes and transformations allow students to manipulate and visualize concepts in real-time.
- Hands-on Construction: Using tools like rulers, compasses, and protractors to construct geometric figures provides a tactile experience of geometric principles.
Interactive Tools for Practice
- Geogebra: A dynamic mathematics software that enables students to explore and visualize algebra and geometry concepts interactively.
- 3D Models: Interactive 3D models allow students to rotate and manipulate objects, providing an in-depth understanding of spatial relationships.
- Online Games: Games focused on geometric shapes and patterns make learning more enjoyable while reinforcing important skills.
Tips for Mastering Geometric Proofs
Mastering logical arguments and proofs is a crucial part of understanding and applying mathematical concepts. These proofs require careful reasoning, step-by-step justification, and a solid grasp of theorems and postulates. Developing proficiency in this area involves more than just memorizing rules; it’s about building a logical framework that connects various ideas and demonstrates relationships between different elements.
Understand the Foundations
Before diving into complex proofs, ensure that you have a strong understanding of basic principles. Theorems, definitions, and postulates form the backbone of any proof, and knowing them inside and out is essential for success. Review key theorems and their applications regularly to keep them fresh in your mind. A clear grasp of these building blocks will make constructing proofs much easier.
Strategic Approaches to Proofs
- Start with what you know: Identify the given information and the end goal of the proof. Breaking down the problem into smaller, manageable parts will help create a clear path toward the solution.
- Work backward: If you’re stuck, try working backward from what needs to be proven. This can often provide insight into the steps required to reach the conclusion.
- Use diagrams: Drawing clear, accurate diagrams is vital in visualizing relationships and making logical connections. They can often reveal hidden relationships and simplify the proof process.
- Write clearly: When presenting a proof, clarity is key. Every step should be justified with a logical explanation, and each transition should be easy to follow. This will ensure that your reasoning is coherent and your argument solid.
Practice Regularly
Practice is one of the best ways to improve in any area, and mastering proofs is no different. The more problems you tackle, the more familiar you will become with different strategies and techniques. Each proof presents a unique challenge, and with consistent practice, your skills will naturally improve over time.
Online Platforms for Geometry Tutoring

With the rise of digital learning, there are now numerous platforms available that offer tutoring services for those looking to enhance their skills in spatial reasoning and related topics. These platforms provide an interactive way to learn, offering personalized support and the ability to learn at one’s own pace. Whether you are struggling with basic concepts or need help with more advanced topics, online tutoring can be a valuable tool for mastering challenging material.
These platforms typically offer a variety of learning resources, including video lessons, practice exercises, quizzes, and one-on-one tutoring sessions. Some even feature live sessions with experienced instructors, allowing for real-time assistance and clarification. Additionally, many platforms offer flexible scheduling, making it easier to fit tutoring sessions around your own schedule.
Visual Aids for Learning Geometry
Using visual tools to understand complex concepts can significantly improve comprehension and retention. When it comes to spatial reasoning and mathematical structures, visuals are especially helpful in bringing abstract ideas to life. By incorporating diagrams, charts, and interactive models, learners can better grasp intricate topics and visualize the relationships between various elements.
Types of Visual Aids
Several types of visual aids can be employed to facilitate learning, each offering unique advantages in breaking down mathematical principles.
- Diagrams: Simple and clear illustrations of shapes and figures are essential for understanding properties and theorems.
- 3D Models: Interactive three-dimensional shapes allow learners to explore depth and perspective, aiding in the understanding of volume and surface area.
- Charts and Graphs: These tools help visualize data and functions, making complex relationships easier to interpret.
- Animations: Moving visuals, such as rotating shapes, can help demonstrate transformations, rotations, and other geometric concepts in dynamic ways.
Benefits of Using Visual Tools
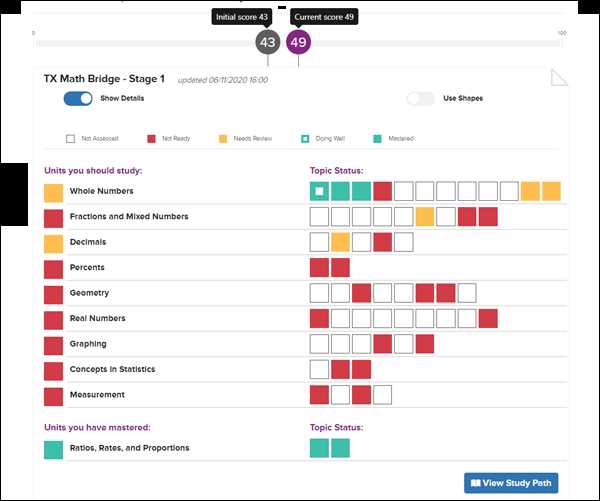
Visual aids engage multiple senses, promoting better retention and understanding. They help students to:
- Enhance spatial awareness by making abstract ideas tangible.
- Improve problem-solving skills by providing a clearer view of how different elements interact.
- Boost confidence as students can visually confirm their understanding of complex concepts.
Geometry Study Strategies for Beginners
Mastering mathematical concepts requires a structured approach, especially for those just starting. With the right study techniques, beginners can build a strong foundation and gain confidence in solving problems. By focusing on understanding core principles, practicing regularly, and breaking down complex problems into simpler steps, students can gradually improve their skills and achieve success.
Key Strategies for Effective Learning
Implementing certain strategies can enhance the learning process and help retain important information. Here are some key approaches:
- Start with Basics: Begin with the fundamental concepts and gradually progress to more complex topics. This ensures a solid understanding of essential principles.
- Practice Regularly: Consistent practice is crucial. Work through problems regularly to reinforce your understanding and improve problem-solving abilities.
- Use Visual Aids: Visual tools, such as diagrams and models, help make abstract concepts more tangible and easier to understand.
- Seek Help When Needed: Don’t hesitate to ask for clarification from teachers, tutors, or peers when faced with difficult concepts.
Building Strong Study Habits
Effective study habits contribute to a deeper understanding and better retention of material. Here are some habits to incorporate:
- Set Clear Goals: Define specific learning objectives for each study session to stay focused and organized.
- Break Down Problems: When facing a complex problem, break it down into smaller, manageable steps to make it easier to solve.
- Review and Reflect: After solving a problem, review the steps taken and reflect on any mistakes made to understand areas for improvement.
- Stay Consistent: Create a study schedule and stick to it to ensure regular and steady progress over time.
How Parents Can Support Geometry Learning
Parents play a crucial role in fostering a supportive environment for their child’s academic growth. When it comes to mastering mathematical concepts, their encouragement, involvement, and understanding can significantly impact a student’s success. By offering practical support, guiding their children through challenges, and fostering a positive attitude towards learning, parents can help strengthen their child’s skills in this subject.
Practical Ways for Parents to Help
There are several ways parents can actively participate in their child’s learning process:
- Create a Positive Study Environment: Ensure that the child has a quiet, well-lit space for studying, free from distractions, where they can focus on their work.
- Encourage Regular Practice: Help your child stay consistent by setting aside time each day to work on exercises and reinforce concepts learned in class.
- Be Patient and Supportive: Understand that learning complex concepts can take time. Provide emotional support, celebrate progress, and be patient with setbacks.
- Show Interest in Their Learning: Ask about their schoolwork, engage in discussions, and express curiosity about their progress to encourage them to stay motivated.
Tips for Effective Communication and Assistance
To further support their child, parents can take these additional steps:
- Review Homework Together: Look over assignments and guide your child through the steps, encouraging them to think critically and work through problems independently when possible.
- Use Real-World Examples: Help your child connect abstract concepts to real-life situations, such as measuring objects, building shapes, or noticing patterns in nature.
- Offer Resources: Provide access to study materials like books, online resources, or tutoring to help clarify difficult concepts and reinforce their learning.
- Maintain Open Communication with Teachers: Stay in touch with your child’s teacher to monitor progress, address concerns, and receive recommendations for additional support.
Using Technology to Enhance Geometry Skills
In today’s digital age, technology offers an array of tools that can significantly improve the way students approach and understand mathematical concepts. Interactive apps, online platforms, and digital resources provide opportunities for practice, visualization, and personalized learning. These tools can make complex topics more accessible and engaging, helping students build a solid foundation in mathematical reasoning.
Key Technology Tools for Learning
Here are some of the most effective tools that can enhance learning in this field:
- Interactive Software: Applications like GeoGebra and Desmos allow students to explore geometric concepts visually. They can manipulate shapes, observe transformations, and better understand spatial relationships in real-time.
- Online Courses and Tutorials: Websites like Khan Academy and Coursera offer structured lessons, video tutorials, and practice exercises tailored to different learning levels, providing a guided approach to mastering concepts.
- Virtual Manipulatives: Platforms that offer virtual tools such as rulers, protractors, and compasses enable students to engage in hands-on activities and experiment with measurements and shapes.
- Mathematical Simulations: Software like Mathway or Wolfram Alpha can solve complex problems step-by-step, helping students understand the process behind solving equations and geometric puzzles.
Benefits of Using Technology

Incorporating technology into the learning process provides several advantages:
- Instant Feedback: Students receive immediate responses to their actions, allowing them to adjust and correct mistakes quickly, leading to better learning outcomes.
- Engagement and Motivation: Interactive tools keep students engaged and motivated by making learning more fun and visually appealing, particularly for those who might struggle with traditional methods.
- Personalized Learning: Many online platforms adapt to a student’s learning pace, providing customized exercises that cater to individual strengths and weaknesses.
- Visual Understanding: Technology aids in visualizing complex geometric concepts, such as the properties of shapes, symmetry, and transformations, making abstract ideas more tangible.


