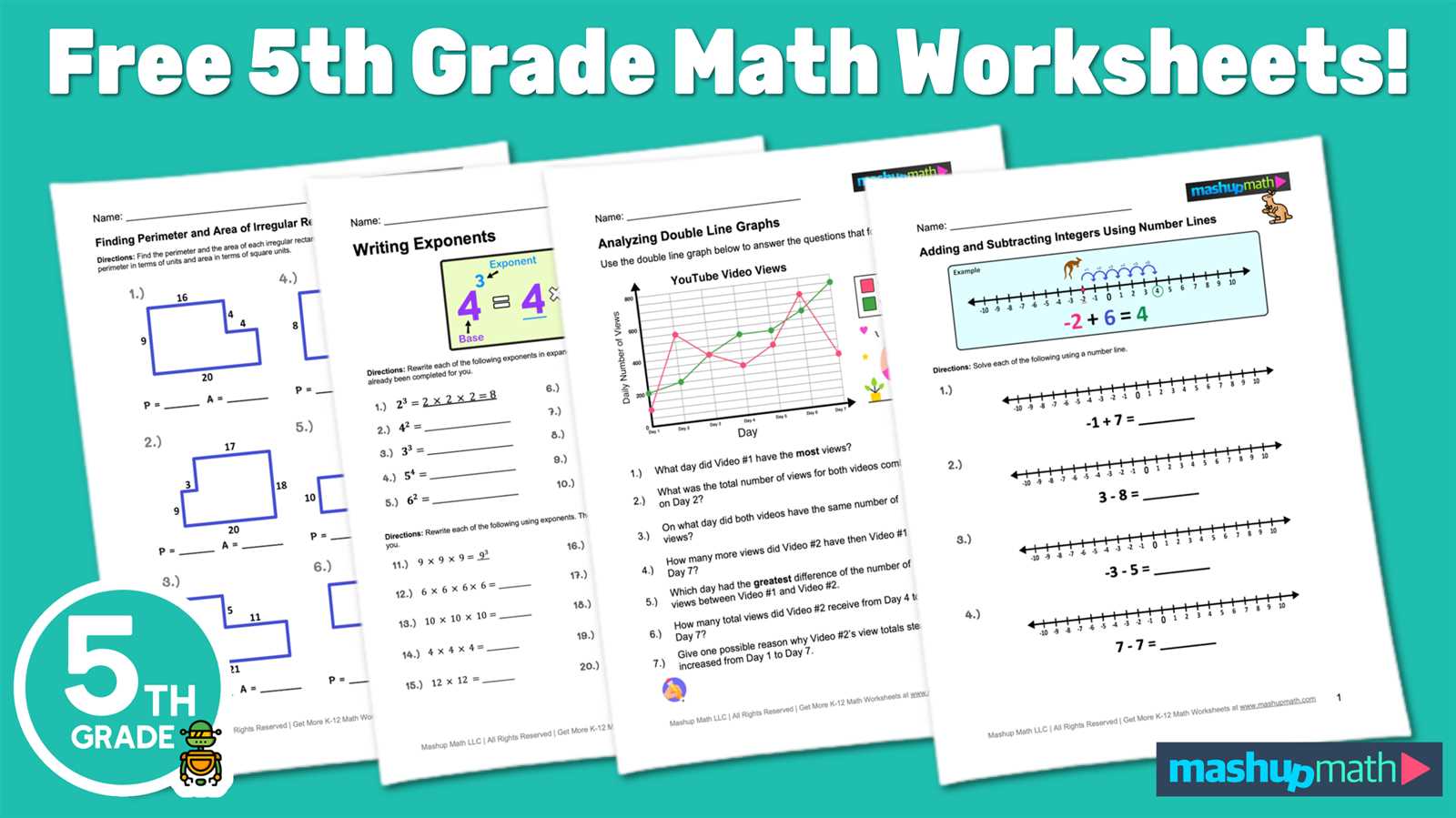
When tackling complex academic material, breaking down each topic into manageable sections is essential for mastering the content. By approaching each concept step by step, students can build a solid foundation and gain a deeper understanding of the subject matter. Whether it’s solving numerical challenges or interpreting problem-solving strategies, a structured approach is crucial for success.
Effective learning often relies on clear explanations and practice. A systematic review of each problem type can help identify recurring patterns and techniques, making it easier to apply knowledge in various situations. With the right guidance, students can improve their skills and approach challenging tasks with confidence.
Strengthening problem-solving abilities is not only about finding the correct solution but also about developing the mindset to approach problems creatively and logically. This approach helps foster both comprehension and retention, turning difficulties into opportunities for growth.
Texas Go Math Volume 2 5th Grade Answers

In this section, we will explore a variety of problem-solving techniques and strategies designed to help students succeed in their studies. It is essential to understand the core principles behind each task in order to apply the most effective methods to arrive at the correct solutions. By working through different types of exercises, students can strengthen their skills and develop a clearer understanding of key concepts.
Mastering Problem-Solving Skills
Effective problem-solving begins with breaking down each question into smaller, more manageable parts. Recognizing patterns and understanding the fundamental rules that govern each type of problem is key to finding accurate solutions. It is important to practice regularly to build confidence and proficiency. The more you work through each problem, the more intuitive the approach becomes.
Building Confidence in Complex Tasks
Developing confidence in solving complex tasks involves both persistence and a strategic approach. As students familiarize themselves with different problem types, they can learn to approach more difficult questions with a calm and methodical mindset. This will ultimately lead to improved results and a stronger grasp of the subject matter.
Overview of Texas Go Math Curriculum

The curriculum is designed to provide students with a structured approach to mastering essential concepts. By focusing on key skills and progressively building on foundational knowledge, it ensures that learners develop both confidence and competence in their studies. The content covers a wide range of topics, each aimed at reinforcing core principles and preparing students for more advanced problem-solving tasks.
The curriculum is divided into several units, each targeting different areas of learning. These units are structured to help students grasp complex topics step by step, ensuring they build a comprehensive understanding over time. Below is a table outlining the main areas covered in the curriculum:
| Unit | Focus Area |
|---|---|
| Unit 1 | Understanding Numbers and Operations |
| Unit 2 | Fractions and Decimals |
| Unit 3 | Geometry and Measurement |
| Unit 4 | Data and Probability |
| Unit 5 | Problem-Solving Strategies |
By following this approach, the curriculum not only teaches mathematical techniques but also encourages logical thinking, problem-solving, and analytical skills. This comprehensive method helps prepare students for real-world challenges and builds a strong foundation for further academic growth.
Key Concepts Covered in Volume 2
This section introduces the core topics explored in the second part of the curriculum, which is designed to deepen students’ understanding and problem-solving skills. Each concept is built on foundational knowledge, allowing learners to expand their capabilities and tackle more complex tasks. By mastering these key ideas, students are better equipped to approach various types of challenges and succeed in their studies.
The following are the main concepts covered:
- Fractions and Decimals: Learning how to convert, compare, and operate with fractions and decimal numbers.
- Geometry: Understanding shapes, angles, and the properties of figures in both 2D and 3D space.
- Measurement: Exploring units of measurement for length, weight, capacity, and time, and applying them in real-life scenarios.
- Problem-Solving Strategies: Developing methods for approaching and solving word problems, including multi-step calculations.
- Patterns and Relationships: Identifying and using patterns in numbers and operations to simplify problems.
These topics are carefully structured to gradually increase in complexity, ensuring that students gain confidence as they progress. Through consistent practice and application of these concepts, learners build critical thinking and analytical skills that are essential for future academic success.
How to Approach Math Problems Effectively
To solve mathematical challenges efficiently, it’s important to develop a systematic approach. Breaking down each problem into smaller, manageable parts allows for better understanding and clearer thinking. This method helps to avoid confusion and ensures that every step is completed accurately. With the right mindset and techniques, any problem can be approached logically, leading to a solution.
Step-by-Step Strategy
Start with understanding the problem. Carefully read each question to ensure you comprehend what is being asked. Identify the key information and determine what needs to be found. Once you have a clear grasp of the task, plan your approach before jumping into calculations.
Organize and Simplify
Simplifying complex problems can often make them more manageable. Break down large problems into smaller steps, and tackle each one separately. If you encounter any obstacles, pause to review the steps and adjust your approach. Taking your time and organizing your work reduces the likelihood of making errors and ensures clarity in your solutions.
Step-by-Step Guide for Answering Questions
Answering complex questions requires a clear and structured approach. By breaking down each problem into manageable steps, students can systematically tackle challenges and ensure they are addressing every aspect of the question. This method not only improves accuracy but also builds confidence in problem-solving.
Understanding the Question
The first step is to carefully read and understand what is being asked. Focus on the key details and requirements. Identify any numbers, operations, or specific instructions provided in the problem. Once you have a clear understanding of the question, you can move on to the next step with confidence.
Organizing the Work
Breaking down the problem into smaller, organized steps is crucial. Start by writing down any important information or formulas that may be needed. Plan how you will approach the solution, whether through calculation, drawing diagrams, or applying specific rules. By keeping the work organized, you minimize the chance of making mistakes and ensure that all parts of the question are addressed.
Common Mistakes to Avoid in Math
When solving numerical problems, it’s easy to make small errors that can lead to incorrect results. Recognizing common mistakes and learning how to avoid them is an important part of improving problem-solving skills. By understanding these frequent pitfalls, students can develop a more accurate and efficient approach to their work.
Common Errors and How to Avoid Them
- Misreading the Question: Always read the problem carefully before starting. Missing a key detail can lead to confusion and incorrect answers.
- Skipping Steps: It’s important to follow each step methodically. Skipping calculations or steps can cause mistakes that might not be immediately obvious.
- Incorrectly Applying Formulas: Double-check the formulas you use to solve problems. Even small mistakes in applying them can result in the wrong solution.
- Forgetting to Check Work: Always review your solution to ensure that it makes sense. Revisiting calculations can help catch errors that might have been overlooked.
Strategies for Improving Accuracy

Developing a consistent approach to problem-solving is essential for avoiding mistakes. Start by organizing your work clearly and check your calculations regularly. Taking the time to carefully follow each step will ensure better results and improve overall confidence in your skills.
Interactive Learning Tools for 5th Graders

Interactive tools provide students with engaging ways to learn complex concepts through hands-on experiences. These resources help make learning more enjoyable and effective by allowing students to visualize problems, practice skills, and receive instant feedback. By using these tools, students can strengthen their understanding while developing critical thinking abilities in a fun and dynamic environment.
Benefits of Interactive Learning
Engagement and Motivation: Interactive tools often make learning more interesting by offering activities that capture students’ attention. This increased engagement motivates students to explore topics in greater depth and develop a deeper understanding of the subject matter.
Instant Feedback: Many interactive tools provide immediate feedback on students’ responses, helping them identify areas for improvement. This allows learners to correct mistakes right away and reinforces correct strategies, which helps improve overall performance.
Popular Interactive Tools
- Digital Simulations: Tools that simulate real-world problems and scenarios, allowing students to experiment and apply concepts in a controlled environment.
- Online Quizzes: Interactive quizzes that provide instant feedback on students’ understanding of topics, helping them reinforce what they have learned.
- Educational Games: Games that incorporate learning objectives, providing students with a fun way to practice skills and problem-solving techniques.
- Interactive Whiteboards: Tools that allow students to collaborate on solving problems, helping them visualize solutions and work through concepts together.
Using these interactive tools in the classroom encourages active learning and ensures that students are able to master new concepts with greater ease. By providing a mix of activities, students are more likely to retain information and feel confident in their abilities.
Helpful Tips for Improving Math Skills
Strengthening mathematical abilities requires consistent practice and the application of effective strategies. By focusing on key areas and developing strong problem-solving habits, students can significantly improve their skills. These tips are designed to help learners build confidence, enhance their understanding, and tackle challenges with greater ease.
Key Strategies for Improvement

- Practice Regularly: Consistency is crucial when it comes to strengthening skills. Set aside time each day to practice different concepts, ensuring that you reinforce what you’ve learned and discover areas that need more attention.
- Break Down Problems: When facing a difficult task, break it down into smaller, manageable steps. This will help you stay organized and reduce the complexity of the problem.
- Understand the Why: Instead of memorizing formulas and procedures, take the time to understand the underlying concepts. This deeper comprehension will help you apply knowledge more effectively in different situations.
- Seek Help When Needed: If you’re struggling with a specific topic, don’t hesitate to ask for help. Whether it’s from a teacher, tutor, or online resource, getting assistance can clarify concepts and prevent confusion.
- Review Mistakes: Analyze the errors you make and learn from them. Understanding why a mistake happened and how to avoid it in the future is essential for improvement.
Additional Tips for Success
- Use Visual Aids: Visual tools such as graphs, diagrams, and charts can help you better understand abstract concepts and make complex problems easier to solve.
- Stay Positive: Maintain a positive attitude toward learning. Confidence can make a huge difference in tackling difficult problems and achieving success.
- Work with Peers: Study groups or peer collaborations can provide different perspectives and help you solve problems more effectively.
By incorporating these strategies into daily practice, students can steadily improve their mathematical abilities and approach challenges with greater ease and confidence.
Understanding Word Problems in Math
Word problems can often seem challenging, but with the right approach, they become manageable. These problems present mathematical concepts in real-world situations, requiring students to extract important information and apply it to solve questions. Developing strategies for understanding and breaking down word problems is key to mastering them and improving problem-solving skills.
Steps to Solve Word Problems
- Read the Problem Carefully: Start by reading the problem at least twice. Ensure you understand all the details, including the question and the data provided.
- Highlight Key Information: Identify and underline the important numbers, terms, and instructions. This helps focus on the necessary elements needed for solving the problem.
- Decide on the Operation: Think about what type of operation is needed–addition, subtraction, multiplication, or division. Often, the wording will give you clues about which operation to use.
- Write an Equation: Translate the word problem into a mathematical equation or expression. This step will make it easier to apply the correct procedures and reach a solution.
- Solve the Problem: Perform the calculations based on your equation. Take your time to ensure accuracy at each step.
- Check Your Work: After solving, review your answer to ensure it makes sense in the context of the problem.
Common Challenges in Word Problems
- Misinterpreting the Question: Sometimes, the question may be disguised with extra information or tricky wording. Always focus on what is being asked, not just the numbers.
- Overlooking Units: Pay attention to units such as time, distance, or quantity. Failing to consider the units can lead to incorrect answers.
- Confusing Operations: Words like “total,” “difference,” and “product” indicate specific operations. Understanding these key terms can help prevent mistakes.
By following these steps and practicing regularly, students can improve their ability to tackle word problems efficiently and confidently. Word problems not only enhance math skills but also help in developing critical thinking abilities for real-world situations.
How to Solve Fractions and Decimals

Understanding how to work with fractions and decimals is essential for mastering various mathematical concepts. Both of these forms of numbers are used to represent parts of a whole, but each has its unique method of manipulation. Being able to convert, compare, and perform operations with fractions and decimals is fundamental for solving many types of problems.
Solving Fractions
- Adding and Subtracting Fractions: To add or subtract fractions, they must have the same denominator. If the denominators are different, find the least common denominator (LCD) and convert the fractions before performing the operation.
- Multiplying Fractions: Multiplication of fractions is straightforward–simply multiply the numerators (top numbers) and the denominators (bottom numbers) together. Simplify the result if possible.
- Dividing Fractions: To divide fractions, multiply by the reciprocal of the second fraction. This means flipping the second fraction upside down before multiplying.
- Simplifying Fractions: After any operation, it’s important to simplify the fraction if possible. Divide both the numerator and the denominator by their greatest common divisor (GCD) to get the simplest form.
Solving Decimals
- Adding and Subtracting Decimals: Align the decimal points before adding or subtracting. Ensure that each decimal has the same number of digits after the decimal point by adding zeroes if necessary.
- Multiplying Decimals: Multiply as if the numbers were whole numbers. After multiplying, count the total number of decimal places in both factors and place the decimal point in the product accordingly.
- Dividing Decimals: To divide a decimal by a whole number, proceed as with long division. If dividing by another decimal, move the decimal points in both numbers to the right to make the divisor a whole number, then proceed with the division.
By practicing these steps, students can develop a solid understanding of how to handle fractions and decimals in various mathematical situations. Regular practice will enhance problem-solving skills and increase confidence in working with both types of numbers.
Mastering Geometry in Volume 2
Geometry is a crucial branch of mathematics that deals with shapes, sizes, and the properties of space. Mastering geometric concepts is essential for building a strong foundation in problem-solving, as it helps students understand the relationships between different figures and their measurements. In this section, we will explore key geometric principles, including measuring angles, working with different shapes, and understanding spatial relationships.
Key Concepts in Geometry
- Angles: Understanding how to measure and classify angles is fundamental. Angles are formed by two rays with a common endpoint, and they can be acute, obtuse, or right angles.
- Shapes and Properties: Recognizing the properties of various shapes such as triangles, quadrilaterals, and circles is vital. This includes knowing the number of sides, angles, and symmetry of each shape.
- Area and Perimeter: Calculating the area and perimeter of shapes is an important skill. These measurements help determine the space occupied by a figure and the length of its boundary.
- Volume: Understanding the concept of volume is key when working with 3D shapes. Volume measures the amount of space a solid object occupies.
Geometry in Action
When solving geometric problems, it’s important to use visual aids, such as diagrams and models, to help identify relationships between figures. Below is a simple table to guide the calculation of area and perimeter for basic shapes:
| Shape | Area Formula | Perimeter Formula |
|---|---|---|
| Rectangle | Area = length × width | Perimeter = 2(length + width) |
| Triangle | Area = ½ × base × height | Perimeter = side1 + side2 + side3 |
| Circle | Area = π × radius² | Perimeter = 2π × radius |
By mastering these concepts and regularly practicing problem-solving strategies, students can build their confidence in geometry. This understanding will not only help in academic settings but also in real-world applications involving spatial awareness and design.
Strategies for Solving Multiplication Problems

Multiplication is a fundamental arithmetic operation that forms the basis for more complex mathematical calculations. Understanding various strategies for solving multiplication problems can help students increase their speed, accuracy, and confidence when dealing with larger numbers. In this section, we will explore different techniques that can simplify multiplication tasks, making them more manageable and less intimidating.
Break Down Large Numbers
One effective strategy for multiplying large numbers is to break them down into smaller, more manageable parts. This method is called “partial products” or “distributive property.” By separating the numbers into tens and ones (or higher place values), you can multiply each part separately and then add the results together.
- Example: Multiply 42 by 36. Break 42 into 40 and 2, and 36 into 30 and 6.
- First, multiply 40 × 30 = 1200
- Then, multiply 40 × 6 = 240
- Next, multiply 2 × 30 = 60
- Finally, multiply 2 × 6 = 12
- Add the results: 1200 + 240 + 60 + 12 = 1512
Use the Commutative Property
The commutative property of multiplication states that changing the order of the numbers does not affect the result. This can be particularly useful when multiplying numbers that are difficult to remember in their current order. Re-arranging the numbers in a way that makes mental calculation easier can save time and reduce errors.
- Example: To multiply 6 × 48, it may be easier to multiply 48 × 6 instead of 6 × 48.
- First, break 48 into 50 – 2. Then, multiply 50 × 6 = 300, and -2 × 6 = -12.
- Add the results: 300 – 12 = 288.
By using these strategies, you can solve multiplication problems more efficiently and with greater accuracy. Regular practice of these techniques will improve problem-solving speed, making multiplication tasks much simpler to tackle.
Using Division Techniques with Confidence
Division can often be a challenging concept, but with the right techniques, it can become much easier to handle. By approaching division problems with a systematic strategy, students can solve complex problems confidently and efficiently. In this section, we will explore different division methods and tips that can help break down problems into more manageable steps, boosting both accuracy and speed.
Long Division Method
The long division method is a classic approach for dividing large numbers. It involves dividing the dividend by the divisor, breaking the process into smaller, more manageable steps. While this method can seem lengthy, it provides a clear and organized way to arrive at the correct quotient.
- Example: Divide 654 by 3.
- Start by dividing the first digit (6) by 3. The result is 2, so write 2 above the line.
- Multiply 2 by 3, which equals 6. Subtract 6 from 6, leaving 0.
- Bring down the next digit (5) and divide 5 by 3. The result is 1, so write 1 above the line.
- Multiply 1 by 3, which equals 3. Subtract 3 from 5, leaving 2.
- Bring down the last digit (4) and divide 24 by 3. The result is 8.
- The final answer is 218, as the remainder is 0.
Dividing by Estimation
When dealing with division problems that seem difficult, estimation can be a valuable tool. By rounding numbers to the nearest ten, hundred, or thousand, students can estimate the quotient and check if their long division results are reasonable. This technique can serve as a quick way to verify answers before performing detailed calculations.
- Example: Divide 877 by 22.
- Estimate by rounding 877 to 880 and 22 to 20. Divide 880 by 20 to get an estimated quotient of 44.
- Use this estimate to guide the actual division process, ensuring the result is reasonable.
By mastering these division techniques, students can approach division problems with greater confidence, making the process quicker and less daunting. With practice, both the long division method and estimation strategies will become second nature.
Exploring Measurement and Data Concepts
Understanding the concepts of measurement and data is essential for making sense of the world around us. These concepts allow us to quantify, compare, and analyze different aspects of daily life, from the dimensions of an object to the patterns in collected information. In this section, we will explore various methods for measuring quantities and analyzing data, helping students build strong foundations in these crucial areas.
Measurement of Length, Weight, and Volume

Measurement is fundamental in both everyday activities and scientific exploration. It involves determining the size, weight, or volume of objects using appropriate units. Different types of measurement units are used depending on what is being measured, such as meters for length, grams for weight, and liters for volume.
| Type of Measurement | Unit of Measure |
|---|---|
| Length | Meter (m), Centimeter (cm), Kilometer (km) |
| Weight | Gram (g), Kilogram (kg), Pound (lb) |
| Volume | Liter (L), Milliliter (mL), Gallon (gal) |
By familiarizing yourself with these units and how to convert between them, you can approach measurement tasks with accuracy and confidence. Mastery of this concept is crucial for tasks ranging from cooking recipes to solving real-world problems in engineering or design.
Analyzing Data: Representing and Interpreting Information
Once data is collected, the next step is analyzing and interpreting it. This involves organizing data into charts, graphs, or tables, making it easier to identify trends, patterns, and relationships. Bar graphs, line plots, and pie charts are common tools used to represent data visually, helping to summarize large sets of information at a glance.
- Bar Graphs: Useful for comparing different categories.
- Line Graphs: Ideal for showing changes over time.
- Pie Charts: Great for displaying parts of a whole.
Accurate data analysis helps in decision-making, whether in science, business, or everyday life. Understanding how to read and interpret graphs and tables is a critical skill that supports logical reasoning and data-driven conclusions.
By mastering both measurement techniques and data analysis, students can develop strong problem-solving skills and gain confidence in applying these concepts in various contexts.
Importance of Practice and Repetition
Mastering any skill, especially in the realm of problem-solving, requires consistent effort and repeated engagement. Practice is a critical component of learning, allowing individuals to internalize concepts and refine their techniques over time. Through repeated exercises, students become more comfortable with new material, gradually building confidence and fluency in applying what they’ve learned.
Building Confidence Through Repetition
Repetition reinforces the neural pathways involved in learning. When a concept or process is practiced multiple times, it becomes easier to recall and apply. This is especially true for subjects that involve step-by-step solutions or computations, where familiarity with the process increases efficiency and accuracy.
- Improves retention: Repetition helps commit concepts to long-term memory.
- Reduces errors: Frequent practice minimizes common mistakes.
- Increases speed: Regular practice helps students solve problems more quickly.
Effective Strategies for Practice
While repetition is essential, it’s important that practice be structured and purposeful. Simply repeating the same task without variation may lead to boredom and stagnation. Instead, consider the following strategies:
- Vary problem types: Work on different types of problems to strengthen understanding from multiple angles.
- Focus on weak areas: Spend extra time on challenging concepts to improve mastery.
- Time yourself: Adding a time element can help build both speed and accuracy.
By integrating these strategies into regular study habits, students can ensure that their practice sessions are both productive and engaging. The goal is not just to complete tasks but to understand the underlying principles and develop the skills needed for independent problem-solving.
Parents’ Role in Supporting Learning
Parents play an essential role in fostering a positive learning environment and supporting their child’s educational journey. Their involvement can significantly influence a child’s attitude toward learning and their ability to understand complex concepts. Whether providing guidance, encouragement, or creating a conducive study environment, parents are integral in helping their children succeed academically.
Creating a Supportive Learning Environment
A key aspect of parental involvement is establishing a study routine that is both structured and flexible. A quiet, distraction-free space allows children to focus and engage with their tasks more effectively. Additionally, providing access to necessary learning tools and resources can further enhance a child’s ability to grasp new material.
- Designate a quiet study area: A clutter-free space promotes concentration.
- Provide necessary resources: Ensure that children have access to textbooks, writing tools, and digital resources when needed.
- Encourage breaks: Short breaks between study sessions help prevent burnout.
Active Involvement in Learning

Being actively engaged in a child’s education does not mean doing their homework for them. Instead, parents should focus on guiding their child through challenges, asking questions to stimulate critical thinking, and helping them find resources when they struggle. Offering praise and motivation also plays a significant role in maintaining a child’s enthusiasm for learning.
| Role | Example |
|---|---|
| Providing guidance | Helping with problem-solving without giving direct answers. |
| Encouraging perseverance | Motivating children to keep trying even when tasks seem difficult. |
| Providing emotional support | Offering reassurance and praise to build self-confidence. |
Through active participation, parents help instill a sense of responsibility and self-motivation in their children. By offering the right balance of support and independence, they prepare their children not only for academic success but also for life beyond school.
Where to Find Additional Learning Resources
When students need extra practice or a different perspective on a topic, there are many resources available outside the traditional classroom materials. These resources can help reinforce concepts, provide additional explanations, and offer interactive activities to boost understanding. Parents, teachers, and students can turn to both online platforms and physical materials to access helpful tools tailored to various learning styles.
Online platforms offer a wealth of interactive activities, videos, and practice problems. Many websites feature tutorials and step-by-step solutions to difficult problems, which can be invaluable for students struggling with specific concepts. Additionally, educational apps and websites often include quizzes and games designed to make learning enjoyable and engaging.
Printed resources such as workbooks, reference books, and practice sheets are also valuable tools. These materials are often aligned with current educational standards and can provide targeted practice to help students master challenging topics.
For those seeking structured guidance, tutoring services–both online and in-person–can offer personalized support tailored to the student’s pace and learning needs. Many local libraries also offer free tutoring sessions or access to educational resources that students can use outside of regular school hours.
Benefits of Reviewing Learning Solutions
Reviewing solutions to various problems is an essential part of the learning process. It not only helps solidify understanding but also allows students to identify areas of improvement. By going over the correct steps and comparing them with their own work, learners can enhance their problem-solving strategies and gain greater confidence in their abilities. This practice fosters critical thinking and helps reinforce concepts that may have been initially challenging.
Key Advantages of Reviewing Solutions
- Reinforces Understanding: Going over solutions helps clarify any misunderstandings and strengthens comprehension of key concepts.
- Improves Accuracy: By identifying errors, students can pinpoint where they went wrong and learn to avoid similar mistakes in the future.
- Builds Confidence: Understanding the correct methods and seeing progress in problem-solving boosts a student’s confidence in their abilities.
- Enhances Retention: Repetition of problem-solving techniques through solution review aids long-term memory retention.
- Identifies Weak Areas: Regular review helps highlight specific areas where students need further practice or clarification.
Effective Strategies for Reviewing Solutions
- Work Through Examples: Take time to review a variety of solved problems to understand the different approaches and strategies used.
- Focus on Mistakes: Examine incorrect answers closely and understand why the mistake occurred. This will help in refining future approaches.
- Use Supplemental Resources: Look for additional explanations or tutorials if needed. Online resources, study groups, or tutoring can provide extra guidance.
- Practice Regularly: Consistent practice and reviewing solutions will enhance mastery over time, leading to more effective learning.